$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$

第１回、第２回、第３回では電磁気学とはどのような学問かを解説してきました。
今回からは、ベクトル解析の復習を行います。

ベクトル演算

図1.1のように、もし$4$km 北へ移動しそのあと$3$km 東に移動すると、合計で$7$km 移動したことになる。しかし、スタート地点からゴール地点の距離は$7$km にはならず、実際の距離は僅か$5$km である。

我々はこのように今までの算数とは明らかに異なる計算規則が必要となる。今までの計算が適用できないのは、今考えている$2$点間を結ぶ要素として大きさ（距離）だけでなく向きも持っているためである。

これらの$2$点間を結んだ、大きさと向きを持つ量をベクトル（vector）と言う。
例えば、速度、加速度、力、運動量などはベクトルである。これに対して、大きさだけを持つ量をスカラー（scalar）と言う。例えば、質量、電荷、密度などはスカラーである。

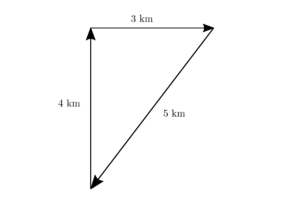
図1.1

古典力学でもそうだったように、ベクトルをあらわす文字を$\bma$、$\bmb$のように太字表記（ボールド体）で、スカラーをあらわす文字を$A$、$B$などのように通常の表記で書くことにする。ベクトル$\bma$の大きさは$|\bma|$、あるいはもっと簡潔に$A$と書くことにする。

ベクトルの図を描くときは、矢のような形で描き、矢の長さをベクトルの長さに対応させて矢の先端をベクトルの向きに対応させる。

図1.2のように、$-\bma$は$\bma$と同じ長さで向きが真逆のベクトルをあらわす。ベクトルは長さと向きという情報は持っているが、位置という情報は持っていないということに注意してほしい。すなわち、長さと向きを変えないならば、ベクトルは自由に動かしても良いことになる。

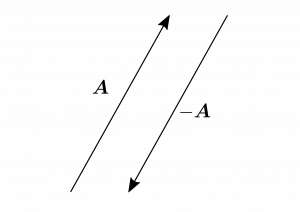
　図1.2

ベクトルに関して、加法則$1$つと積法則$3$つ、計$4$つの演算規則を定義しよう。

(1) 2つのベクトルの加法則

図1.3のように、$\bma$の先端に$\bmb$の末端が来るようにしたとき、和$\bma+\bmb$は$\bma$の末端から$\bmb$の先端までを結ぶベクトルになる。このとき和はどっちを先に足しても良く、

\[
\bma+\bmb=\bmb+\bma
\]

が成り立つ。

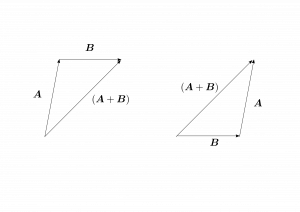
図1.3

更にベクトルを付け足したり、図1.4のように反対向きのベクトルを足したりすることも出来て、
\[
(\bma+\bmb)+\bmc=\bma+(\bmb+\bmc)
\]
\[
\bma-\bmb=\bma+(-\bmb)
\]

が成り立つ。

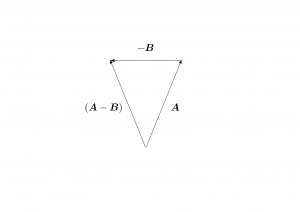
図1.4

(2) スカラーの積法則

正のスカラー$a$をベクトルに掛けると、ベクトルの大きさは$a$倍されて、向きは変わらない。もしも$a$が負であれば、向きは反対方向になる。このスカラーの積は分配することが出来て、
\[
a(\bma+\bmb)=a\bma+a\bmb
\]
が成り立つ。

図1.5

(3) 2つのベクトルの内積

$2$つのベクトルのドットの積は
\[
\bma\cdot\bmb\coloneqq AB\cos{\theta}\tag{1}
\]
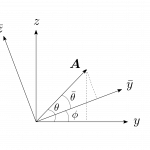
と定義される。このような積を内積という。但し、$\theta$は図1.6のように$2$つのベクトルのなす角である。$\bma\cdot\bmb$はスカラーであることに注意しなければならない。

このように、内積は$2$つのベクトルからスカラーを創るような演算であるため、しばしばスカラー積（scalar product）と呼ばれることもある。内積はどちらを順番に演算しても良く、
\[
\bma\cdot\bmb=\bmb\cdot\bma
\]
が成り立つ。また、分配法則も以下のように成り立つ。
\[
\bma\cdot(\bmb+\bmc)=\bma\cdot\bmb+\bma\cdot\bmc\tag{2}
\]
幾何学的には、$\bma\cdot\bmb$は$\bma$を$\bmb$の方向に射影したときの掛け算、または$\bmb$を$\bma$の方向に射影したときの掛け算をあらわしている。もしも$2$つのベクトルが平行なら$\theta=0$なので$\bma\cdot\bmb=AB$となり、$2$つのベクトルが垂直なら$\theta=\frac{\pi}{2}$なので$\bma\cdot\bmb=0$となる。そして特に$\bma=\bmb$のとき、
\[
\bma\cdot\bma=A^2\tag{3}
\]
が成り立つ。

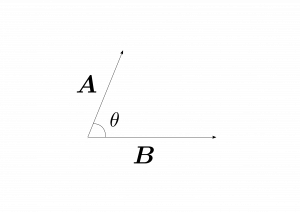
図1.6

例題

図1.7のように、$\bmc=\bma-\bmb$とする。$\bmc\cdot\bmc$を計算せよ。

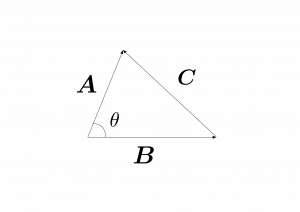
図1.7

解説

以下のように計算する。
\[
\bmc\cdot\bmc=(\bma-\bmb)\cdot(\bma-\bmb)=\bma\cdot\bma-\bma\cdot\bmb-\bmb\cdot\bma+\bmb\cdot\bmb
\]
これを内積の定義と諸法則を用いて整理すると、
\[
C^2=A^2+B^2-2AB\cos{\theta}
\]
となる。これは余弦定理に他ならない。このように、図形の性質に関する公式を自然な形で求めることが出来るのがベクトルの利点である。

• (4) 2つのベクトルの外積

$2$つのベクトルのクロスの積は
\[
\bma\times\bmb\coloneqq AB\sin{\theta}\bm{\hat{n}}\tag{4}
\]
と定義される。これをベクトルの外積という。但し、$\bm{\hat{n}}$はベクトル$\bma$と$\bmb$によって作られる平面と垂直な方向を向いた、大きさが$1$のベクトルである。このように、大きさが$1$のベクトルを単位ベクトル（unit vector）という。

以後、ハット記号を付けたベクトルは全て単位ベクトルをあらわすものとする。

さて、この$\bm{\hat{n}}$の向きには考えている面に関して上向きか下向きかという$2$つの可能性がある。この曖昧さを払拭するために、我々は通常、右ねじの法則という規則を用いる。

つまり、右手を用意して、親指以外の指$4$本を$1$本目のベクトルから$2$本目のベクトルへ小さいほうの角度の周りで回す。このときの親指の向きが$\bm{\hat{n}}$の向きである。図1.8のように、$\bma\times\bmb$の向きは紙面表向きであり、$\bmb\times\bma$の向きは紙面裏向きとなる。

このように、外積は$2$つのベクトルからベクトルを創るような演算であるため、しばしばベクトル積（vector product）と呼ばれることもある。内積のときと同様、外積も以下のように分配法則が適用出来る。
\[
\bma\times(\bmb+\bmc)=(\bma\times\bmb)+(\bma\times\bmc)\tag{5}
\]

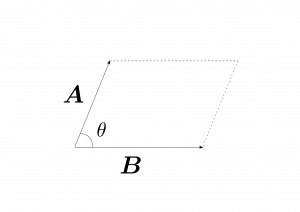
図1.8

しかし、積の順番は交換可能ではない。実際、
\[
(\bmb\times\bma)=-(\bma\times\bmb)\tag{6}
\]
が成り立つ。図1.8のように、幾何学的には、$|\bma\times\bmb|$はベクトル$\bma$と$\bmb$によってつくられる平行四辺形の面積をあらわしている。もしも$2$つのベクトルが平行なら$\theta=0$なので$\bma\times\bmb=\bm{0}$となる。特に、
\[
\bma\times\bma=0
\]
は常に成り立つ。