$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$

第４回に引き続き、ベクトル解析の復習、特にベクトル代数の確認を行います。

ベクトル代数：成分形式

前の小節ではベクトルの演算を定義した。そこでは、特別な座標系を決めることなく、ある意味抽象的に議論をしてきた。実際にはベクトルの成分を議論するためにはCartesian 座標系（直交座標系）$(x,y,z)$を取ることが多い。

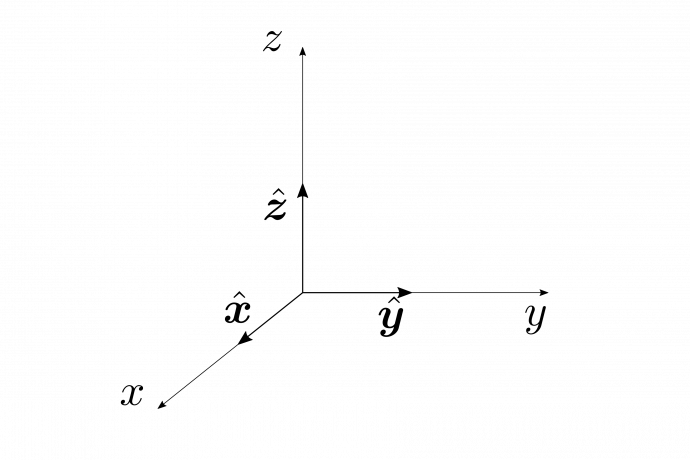
図1.9(a)のように、$x$、$y$、$z$軸と平行になるように単位ベクトル$\bm{\hat{x}}$、$\bm{\hat{y}}$、$\bm{\hat{z}}$を採る。これらを基底ベクトル（basis vectors）という。

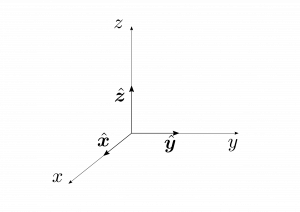
図1.9(a)

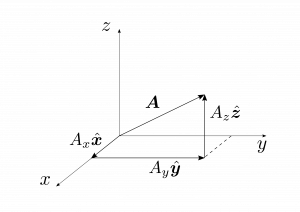
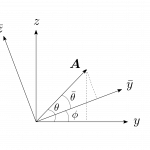
図1.9(b)

任意のベクトル$\bma$は図1.9(b)のようにこれらの基底ベクトルを用いて展開することが出来て、

\[
\bma=A_x\bm{\hat{x}}+A_y\bm{\hat{y}}+A_z\bm{\hat{z}}
\]
となる。$A_x$、$A_y$、$A_z$は$\bma$の成分である。幾何学的には、これらは$\bma$の$3$つの軸の射影成分であり、
\[
A_x=\bma\cdot\bm{\hat{x}},~A_y=\bma\cdot\bm{\hat{y}},~A_z=\bma\cdot\bm{\hat{z}}
\]
が成り立っている。これらのことを用いて、ベクトルの和を具体的な成分で計算し直すと、前の小節での演算法則は次のようにまとめることが出来る。

(1) ベクトルの和は成分ごとの和になる

具体的に計算すると、以下のようになる。
\begin{align}
\bma+\bmb=&(A_x\bm{\hat{x}}+A_y\bm{\hat{y}}+A_z\bm{\hat{z}})+(B_x\bm{\hat{x}}+B_y\bm{\hat{y}}+B_z\bm{\hat{z}})\nonumber\\
=&(A_x+B_x)\bm{\hat{x}}+(A_y+B_y)\bm{\hat{y}}+(A_z+B_z)\bm{\hat{z}}\tag{7}
\end{align}

(2) ベクトルにスカラーを掛けると全ての成分に掛かる

\[
a\bma=(aA_x)\bm{\hat{x}}+(aA_y)\bm{\hat{y}}+(aA_z)\bm{\hat{z}}\tag{8}
\]

(3) 内積は成分ごとの積の和

$\hbx$、$\hby$、$\hbz$は互いに直交した単位ベクトルであるから、

\[
\hbx\cdot\hbx=\hby\cdot\hby=\hbz\cdot\hbz=1,~\hbx\cdot\hby=\hby\cdot\hbz=\hbz\cdot\hbx=0\\\tag{9}
\]
が成り立つ。よって、
\[
\bma\cdot\bmb=(A_x\hbx+A_y\hby+A_z\hbz)\cdot(B_x\hbx+B_y\hby+B_z\hbz)=A_xB_x+A_yB_y+A_zB_z\tag{10}
\]
となる。特に、$\bma\cdot\bma=A_x^2+A_y^2+A_z^2$が成り立つから、
\[
A=\sqrt{A_x^2+A_y^2+A_z^2}\tag{11}
\]
となる。これはPythagoras の定理の一般化であるとみることも出来る。

(4) 外積は$\hbx,\hby,\hbz$と成分で書いた$\bma$、$\bmb$を並べた行列式

内積のときの基底ベクトルの計算と同様に、以下が成り立つ（これらの式は右手系を採用して書いている。左手系を採用した場合は符号が全て反対になる。他の多くの本に合わせて、以下、右手系を一貫して用いることにする。）。
\[
\left\{
\begin{array}{rcrclcc}
\hbx\times\hbx&=&\hby\times\hby&=&\hbz\times\hbz&=&\bm{0}\\
&&&&&&\\
\hbx\times\hby&=&-\hby\times\hbx&=&\hbz&&\\
&&&&&&\\
\hby\times\hbz&=&-\hbz\times\hby&=&\hbx&&\\
&&&&&&\\
\hbz\times\hbx&=&-\hbx\times\hbz&=&\hby&&\\
\end{array}
\right.
\tag{12}
\]
従って、
\begin{align}
\bma\times\bmb=&(A_x\hbx+A_y\hby+A_z\hbz)\times(B_x\hbx+B_y\hby+B_z\hbz)\nonumber\\
=&(A_yB_z-A_zB_y)\hbx+(A_zB_x-A_xB_z)\hby+(A_xB_y-A_yB_x)\hbz\tag{13}
\end{align}
と分かる。この厄介な表式は以下のようにきれいな形で書くことが出来る。
\[
\bma\times\bmb=\left|
\begin{array}{ccc}
\hbx&\hby&\hbz\\
A_x&A_y&A_z\\
B_x&B_y&B_z
\end{array}
\right|\tag{14}
\]

但し、この行列式はあくまでも「観賞用」であることに注意せよ。具体的な計算を実行するときは、(1.13)の式を利用する必要がある。

例題

図1.10において、$\bma$と$\bmb$のなす角を求めよ。

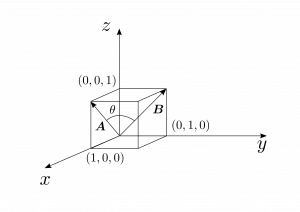
図1.10

解説

$\bma$と$\bmb$はそれぞれ、
\[
\bma=1\hbx+0\hby+1\hbz=(1,0,1),~\bmb=0\hbx+1\hby+1\hbz=(0,1,1)
\]
なので、これらの内積を$2$通りの形で計算すると、
\[
\left\{
\begin{array}{rcl}
\bma\cdot\bmb&=&AB\cos{\theta}=\sqrt{2}\sqrt{2}\cos{\theta}=2\cos{\theta}\\
&&\\
\bma\cdot\bmb&=&1\cdot0+0\cdot1+1\cdot1=1\\
\end{array}
\right.
\]
よって、$\theta=\pi/3$である。

勿論、今の問題は簡単な問題だから、$\bma+\bmb$という矢印を引くことで正三角形が作れて、$\theta=\pi/3$を簡単に見出すことが出来るであろう。

しかし、より複雑な問題では、絵を描くだけで角度を求めることは出来なくなってしまう。このようなときにこそ、内積の計算によって角度を求めるという方法は真価を発揮するのである。