$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

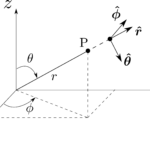
位置ベクトル、変位ベクトル、間隔ベクトル

$3$次元におけるある点の位置は、Cartesian 座標$(x,y,z)$を並べることで記述することが出来る。図1.13のように、原点$\mathcal{O}$から点までを結んだベクトルを位置ベクトル（position vector）という。この位置ベクトル$\bmsr$は、以下のように書ける。

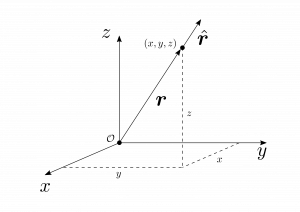
図1.13

今後$\bmsr$と書くときは常にこのような意味で書くことにする。そして、その大きさは

である。これは当然原点からの距離をあらわしている。また、

は動径方向の外側を向いた単位ベクトルをあらわしている。$(x,y,z)$にある点が$(x+\rmd x,y+\rmd y,z+\rmd z)$へ微小変位したときの微小変位ベクトル（infinitesimal displacement vector）は

と書くことにする（そのまま$\rmd \bmsr$と書けるのだが、微小変位においては特別な表記をする方が便利なのである。）。

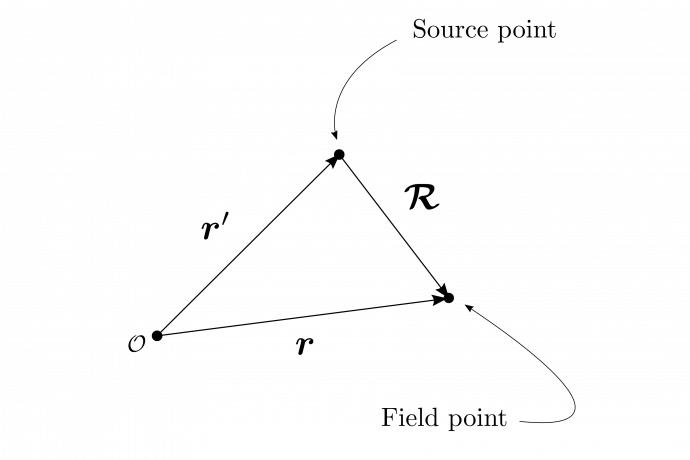
図1.14のように電磁気学では、電荷が位置している源泉の点$\bmsr’$と、考えている問題の中で電場や磁場の計算をしなければならないから、場の点$\bmsr$という$2$点を含む問題に頻繁に遭遇することになる。源泉の点から場の点までの間隔ベクトルをあらわす略記法として筆記体$\bcar$を

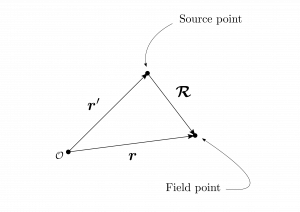
図1.14

直交座標では、

となる。これらの式で複雑な部分は$\bcar$、$\car$、$\hcar$で簡単に書くことが出来た。$\car$記法のご利益がこれで理解出来たはずである。