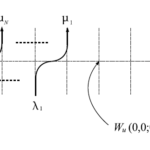
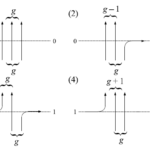
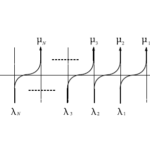
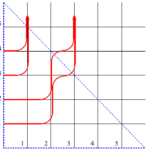
非対称排他過程の概略

非対称排他過程（Asymmetric Exclusion Process）の典型的な例として、1次元格子上に粒子がいっぱいいるとして、各粒子が確率的に移動するという問題を考える。粒子は次の2つのルールに従って移動する。

• 各粒子は各時刻で、もし右隣のサイトが空いている場合に限り、確率$p$で飛び移る。
• もし右隣のサイトが他の粒子に占有されていたら、飛び移ることは出来ない。

2番目のルールが排他的相互作用に対応している。下図では説明の都合上、3個の粒子を描いている。

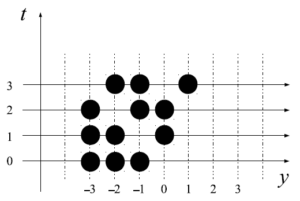
図5　非対称排他過程の例

これは後半にやる非平衡統計力学のモデルであり、Kardar-Parisi-Zhang 普遍クラスと呼ばれる。6頂点模型は平衡統計力学のモデルだったが、実は6頂点模型はKardar-Parisi-Zhang 普遍クラスとつながりがある。

確率的$6$頂点模型の概略

確率的6頂点模型とは6頂点模型の一種である。まず、後の便宜のために次のような略記法を更に導入する。

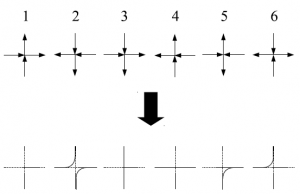
図6　確率的6頂点模型の略記図

そして、$0\leq\delta_1<1$、$0\leq\delta_2<1$を用いて$(\omega_1,\omega_2,\omega_3,\omega_4,\omega_5,\omega_6)=(1,1,\delta_1,\delta_2,1-\delta_1,1-\delta_2)$とする。これが確率的6頂点模型の設定である。境界条件のある$\mathbb{Z}^2_{\geq1}$上の確率6頂点模型を、簡単のために$\delta_1=0$として考えよう。

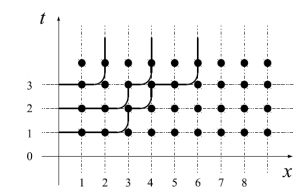
図7　境界条件のある$\mathbb{Z}^2_{\geq1}$上の確率的6頂点模型（$\delta_1=0$）

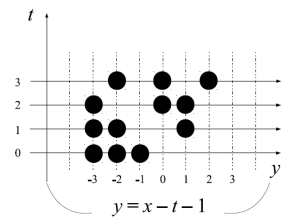
図8　図7に対応したランダムウォークの図

右側の粒子から順に粒子を粒子A、B、C と名付ける。

粒子A は$t$が$0\rightarrow1$となるときに$\delta_2^2(1-\delta_2)$、$1\rightarrow2$となるときに$(1-\delta_2)$、$2\rightarrow3$となるときに$\delta_2(1-\delta_2)$という重みになる。

粒子B は$0\rightarrow1$となるときは排他効果で$1$になる。$t$が$1\rightarrow2$となるときに$(1-\delta_2)$、$2\rightarrow3$となるときは排他効果で$1$になる。

粒子C は$t$が$0\rightarrow1$となるときと$1\rightarrow2$となるときは排他効果で$1$になる。$2\rightarrow3$となるときに$\delta_2(1-\delta_2)$という重みになる。

確率的6頂点模型は前小節で説明したモデルと違って1マス以上飛び移ることが出来ているが、これも非対称排他過程の1種である。