$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}$

モノドロミー行列

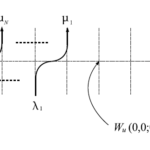
図24 $6$頂点模型の略記図

モノドロミー行列とは、一言で言ってしまえば$T$のことである。これについてもう少し考えてみよう。ここでは$z=0$として話を進めていく。以前定義したように、

\begin{equation}
T(u)=L_M(u)L_{M-1}(u)\cdots L_1(u)=R_{0M}(u)R_{0M-1}(u)\cdots R_{01}(u) ,
\end{equation}
\begin{equation}
T(u)\in\mathrm{End}(V_0\otimes _1\otimes\cdots V_M)
\end{equation}

であるが、最初の$V_0$について

\begin{equation}
T(u)=\left(
\begin{array}{cc}
A(u)&B(u)\\
C(u)&D(u)
\end{array}
\right)
\end{equation}

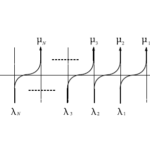
という形で行列表示する。但し、各要素は行列になっており、行・列共に$1$が$\rightarrow$、$2$が$\leftarrow$に対応している。つまり$A(u)$から$D(u)\in\mathrm{End}(V_1\otimes\cdots\otimes V_M)$は$2^\times2^M$行列である。例えば、$A(u)$の成分は

\begin{equation}
(A)^{a_1b_1,a_2b_2,\cdots,a_Mb_M}=R^{1z,a_Mb_M}R^{z_1z_2,a_{M-1}b_{M-1}}\cdots R^{Z_{M-1}1,a_1b_1}
\end{equation}

となる。これを絵で描くと図25のようになる。

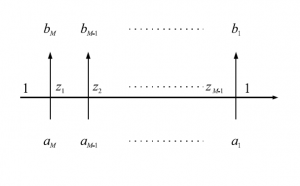
図25 $6$頂点模型の略記図

さて、我々は転送行列$\mathcal{T}(u)$を対角化したかった訳だから、$\mathcal{T}(u)$は今、
\begin{equation}
\mathcal{T}(u)=\mathrm{Tr}T(u)=A(u)+D(u)\tag{7}
\end{equation}
となることに注意すればよい。ここでは(4)を用いて$A(u)$から$D(u)$の関係式を求めることを考えよう。(4)の両辺に左から$P_{12}$を掛ける。但し、$P$は$P(x\otimes y)=y\otimes x$という性質をもつのであった。これにより

\begin{align}
P_{12}R_{12}(u-v)T_{13}(u)T_{23}(v)=&P_{12}T_{23}(v)T_{13}(u)R_{12}(u-v)\nonumber\\
=&P_{12}T_{23}(v)P_{12}P_{12}T_{13}(u)P_{12}P_{12}R_{12}(u-v)\nonumber\\
=&T_{13}(u)T_{23}(v)P_{12}R_{12}(u-v)\nonumber
\end{align}

となる。但し、途中で$P_{12}P_{12}=\mathbbm{1}$及び、問題2.4の結果を用いた。従って、

\begin{equation}
\check{R}_{12}(u-v)T_{12}(u)T_{23}(v)=T_{13}(u)T_{23}(v)\check{R}_{12}(u-v)\tag{8}
\end{equation}

と結論出来る。但し、$\check{R}$は今、以下のように定義されている。

\begin{equation}
\check{R}_{12}\coloneqq P_{12}R_{12}(u-v)=\left(
\begin{array}{cccc}
1&0&0&0\\
0&0&1&0\\
0&1&0&0\\
0&0&0&1
\end{array}
\right)\left(
\begin{array}{cccc}
a&0&0&0\\
0&b&c&0\\
0&c&b&0\\
0&0&0&a
\end{array}
\right)=\left(
\begin{array}{cccc}
a&0&0&0\\
0&c&b&0\\
0&b&c&0\\
0&0&0&a
\end{array}
\right)
\end{equation}

これによって、(7})はコンパクトに書くことが出来て、

\begin{equation}
\check{R}(u-v)(T(u)\otimes T(v))=(T(v)\otimes T(u))\check{R}(u-v)\tag{8′}
\end{equation}

とあらわされる。但し、上の$\otimes$は$2\times2$行列の意味でのテンソル積である。この式を具体的な行列で書いてみれば、

\begin{align}
\left(
\begin{array}{cccc}
a(u-v)&0&0&0\\
0&c(\eta)&b(u-v)&0\\
0&b(u-v)&c(\eta)&0\\
0&0&0&a(u-v)
\end{array}
\right)\left(
\begin{array}{cccc}
A(u)A(v)&A(u)B(v)&B(u)A(v)&B(u)B(v)\\
A(u)C(v)&A(u)D(v)&B(u)C(v)&B(u)D(v)\\
C(u)A(v)&C(u)B(v)&D(u)A(v)&D(u)B(v)\\
C(u)C(v)&C(u)D(v)&D(u)C(v)&D(u)D(v)
\end{array}
\right)\nonumber\\
=&\left(
\begin{array}{cccc}
A(v)A(u)&A(v)B(u)&B(v)A(u)&B(v)B(u)\\
A(v)C(u)&A(v)D(u)&B(v)C(u)&B(v)D(u)\\
C(v)A(u)&C(v)B(u)&D(v)A(u)&D(v)B(u)\\
C(v)C(u)&C(v)D(u)&D(v)C(u)&D(v)D(u)
\end{array}
\right)\left(
\begin{array}{cccc}
a(v-u)&0&0&0
0&c(\eta)&b(v-u)&0
0&b(v-u)&c(\eta)&0
0&0&0&a(v-u)
\end{array}
\right)\nonumber\tag{8”}
\end{align}

となる。先程$P_{12}$を入れて計算したのは$13$と$23$の添字が来る順番を両辺でそろえるためであったのだが、その代償として我々は$\check{R}_{12}$を導入することになったのである！さて、この行列の各成分を比較すると成り立つ等式のうち、特に以下の関係式が後で重要となる。

\begin{equation}
\left\{
\begin{array}{rcl}
A(u)B(v)&=&\dfrac{a(v-u)}{b(v-u)}B(v)A(u)-\dfrac{c}{b(v-u)}B(u)A(v)\\
&&\\
D(u)B(v)&=&\dfrac{a(u-v)}{b(u-v)}B(v)D(u)+\dfrac{c}{b(v-u)}B(u)D(v)\\
&&\\
B(v)B(u)&=&B(u)B(v)
\end{array}
\right.\tag{9}
\end{equation}

問題13

(9)を確かめよ。

解答13

与えられた行列の掛け算を各辺計算すると、

\begin{align}
&\left(
\begin{array}{cccc}
a(u-v)&0&0&0\\
0&c(\eta)&b(u-v)&0\\
0&b(u-v)&c(\eta)&0\\
0&0&0&a(u-v)
\end{array}
\right)\left(
\begin{array}{cccc}
A(u)A(v)&A(u)B(v)&B(u)A(v)&B(u)B(v)\\
A(u)C(v)&A(u)D(v)&B(u)C(v)&B(u)D(v)\\
C(u)A(v)&C(u)B(v)&D(u)A(v)&D(u)B(v)\\
C(u)C(v)&C(u)D(v)&D(u)C(v)&D(u)D(v)
\end{array}
\right)\nonumber\\
=&\tiny\left(
\begin{array}{cccc}
a(u-v)A(u)A(v)&a(u-v)A(u)B(v)&a(u-v)B(u)A(v)&a(u-v)B(u)B(v)\\
cA(u)C(v)+b(u-v)C(u)A(v)&cA(u)D(v)+b(u-v)C(u)B(v)&cB(u)C(v)+b(u-v)D(u)A(v)&cB(u)D(v)+b(u-v)D(u)B(v)\\
b(u-v)A(u)C(v)+cC(u)A(v)&b(u-v)A(u)D(v)+cC(u)B(v)&b(u-v)B(u)C(v)+cD(u)A(v)&b(u-v)B(u)D(v)+cD(u)B(v)\\
a(u-v)C(u)C(v)&a(u-v)C(u)D(v)&a(u-v)D(u)C(v)&a(u-v)D(u)D(v)
\end{array}
\right)\nonumber
\end{align}

\begin{align}
&\left(
\begin{array}{cccc}
A(v)A(u)&A(v)B(u)&B(v)A(u)&B(v)B(u)\\
A(v)C(u)&A(v)D(u)&B(v)C(u)&B(v)D(u)\\
C(v)A(u)&C(v)B(u)&D(v)A(u)&D(v)B(u)\\
C(v)C(u)&C(v)D(u)&D(v)C(u)&D(v)D(u)
\end{array}
\right)\left(
\begin{array}{cccc}
a(v-u)&0&0&0\\
0&c(\eta)&b(v-u)&0\\
0&b(v-u)&c(\eta)&0\\
0&0&0&a(v-u)
\end{array}
\right)\nonumber\\
=&\left(
\begin{array}{cccc}
a(v-u)A(v)A(u)&cA(v)B(u)+b(u-v)B(v)A(u)&b(u-v)A(v)B(u)+cB(v)A(u)&a(v-u)B(v)B(u)\\
a(v-u)A(v)C(u)&cA(v)D(u)+b(u-v)B(v)C(u)&b(u-v)A(v)D(u)+cB(v)C(u)&a(v-u)B(v)D(u)\\
a(v-u)C(v)A(u)&cC(v)B(u)+b(u-v)D(v)A(u)&b(u-v)C(v)B(u)+cD(v)A(u)&a(v-u)D(v)B(u)\\
a(v-u)C(v)C(u)&cC(v)D(u)+b(u-v)D(v)C(u)&b(u-v)C(v)D(u)+cD(v)C(u)&a(v-u)D(v)D(u)
\end{array}
\right)\nonumber
\end{align}

となる。従って、$(1,3)$成分、$(2,4)$成分、$(1,4)$成分をそれぞれ比較すれば、所望の式を得る。