$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}
\def\Ket#1{{\left|{#1}\right\rangle}}$
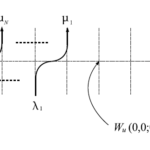
Yang-Baxter 方程式2
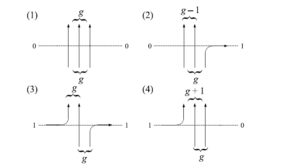
図45 $6$頂点模型の略記図
| $W_u(i_1,j_1;i_2,j_2)$ | $(1)$ | $(2)$ | $(3)$ | $(4)$ |
| $W_u(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{(1-s^2q^{g-1})u}{1-su}$ | $\dfrac{u-sq^g}{1-su}$ | $\dfrac{1-q^{g+1}}{1-su}$ |
| $W_u^c(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{(1-q^g)u}{1-su}$ | $\dfrac{u-sq^g}{1-su}$ | $\dfrac{1-s^2q^g}{1-su}$ |
| $L_u(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{-su(1-q^g)}{1-su}$ | $\dfrac{-s(u-sq^g)}{1-su}$ | $\dfrac{1-s^2q^g}{1-su}$ |
図10を再掲すると、以下のようになっている。
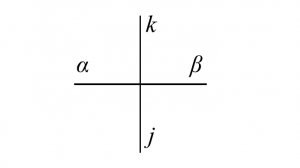
図10 $6$頂点模型の略記図
故に、点線を$1$、実線を$2$とすると、
\begin{equation}
R=(r_{ij}^{\alpha\beta,jk})=\left(
\begin{array}{cccc}
a&0&0&0\\
0&b&c&0\\
0&c&b&0\\
0&0&0&a
\end{array}
\right)
\end{equation}
であったから、例えば$r^{11,22}=b$などとなる。さて、図を考えてみると以下のようになる。但し、黒丸が$X$、矢印が$W$に対応している。
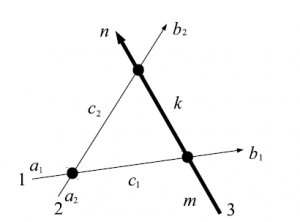
図46 $6$頂点模型の略記図
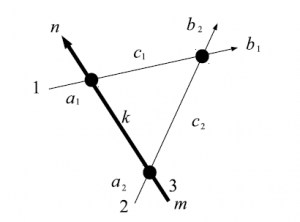
図47 $6$頂点模型の略記図
\begin{equation}
X(a_2,a_1;c_2,c_1)W_{u_1}(m,c_1;k,b_1)W_{u_2}(k,c_2;n,b_2)=W_{u_2}(m,a_2;k,c_2)W_{u_1}(k,a_1;n,c_1)X(c_2,c_1;b_2,b_1)\label{eq:5.1}
\end{equation}
但し、$a_i,b_i\in(0,1)$、$m,n,k\in\{0,1,2,\cdots\}$であり、$c_1,c_2,k$については和を取るものとする。また、$W_u(m,a;n,b)$は図48左図のような状況をあらわしている。太い縦矢印の部分は複数本の矢印が存在することを示している。これが特に$1$本であるならYang-Baxter 方程式に他ならないので、hsvm の式はYang-Baxter 方程式の拡張とみなすことが出来るであろう。
次にオペレーター表示について説明する。これは図48右図のような状況をあらわしたものであり、モノドロミー行列$T(u)\in\mathrm{End}(W\otimes V_0)$を用いた表示法である。但し、$W$は$2$次のベクトル空間$\mathbb{C}\cdots\oplus\mathbb{C}-$であり、$V_0$は$\mathbb{C}\underbrace{\vdots}_{0本}\mathbb{C}\underbrace{\uparrow}_{1本}\oplus\cdots\oplus\mathbb{C}\uparrow$である。
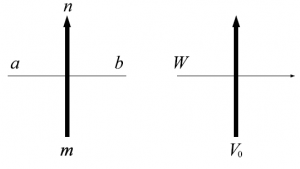
図48 $6$頂点模型の略記図
このとき、オペレーター表示では、
\begin{equation}
T(u)=\left(
\begin{array}{rr}
A_1(u)&C_1(u)\\
B_1(u)&D_1(u)
\end{array}
\right)
\end{equation}
とする。但し、$A_1(u)\sim D_1(u)\in\mathrm{End}(V_0)$である。
さて、$V_0$の$\underbrace{\uparrow\uparrow\cdots\uparrow}_{g本}$に対応する基底を$e_g$と書くことにすると、
\begin{equation}
\left\{
\begin{array}{rcl}
A_1(u):A_1(u)e_g&=&W_u(g,0:g,0)e_g\\
&&\\
B_1(u):B_1(u)e_g&=&W_u(g,1:g+1,0)e_g\\
&&\\
C_1(u):C_1(u)e_g&=&W_u(g,0:g-1,1)e_g\\
&&\\
D_1(u):D_1(u)e_g&=&W_u(g,1:g,1)e_g\\
\end{array}
\right.
\end{equation}
と書くことが出来る。これは図49の絵を基にしている。
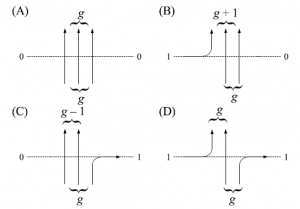
図49 $6$頂点模型の略記図
これは先の$6$頂点模型の$A(u)$から$D(u)$の定義と$B(u)$と$C(u)$の位置が逆になっていることに注意しなければならない。これはどちらに$(1,0)^{\mathrm{T}}$と$(0,1)^{\mathrm{T}}$を割り当てるかという違いでしかないので、本質的なものではない。以下、この定義に従って議論する。$6$頂点模型のときの(8)、(9)と同様に、高次元スピン頂点模型について以下が成立することが分かる。
\begin{equation}
\check{X}(T(u_1)\otimes T(u_2))=(T(u_2)\otimes T(u_1))\check{X}\label{eq:5.2}
\end{equation}
但し、$\check{X}=PX$である。また、$T(u_1)\otimes T(u_2)$は以下のようになっている。
\begin{equation}
T(u_1)\otimes T(u_2)=\left(
\begin{array}{rrrr}
A_1(u_1)A_1(u_2)&A_1(u_1)C_1(u_2)&C_1(u_1)A_1(u_2)&C_1(u_1)C_1(u_2)\\
A_1(u_1)B_1(u_2)&A_1(u_1)D_1(u_2)&C_1(u_1)B_1(u_2)&C_1(u_1)D_1(u_2)\\
B_1(u_1)A_1(u_2)&B_1(u_1)C_1(u_2)&D_1(u_1)A_1(u_2)&D_1(u_1)C_1(u_2)\\
B_1(u_1)B_1(u_2)&B_1(u_1)D_1(u_2)&D_1(u_1)B_1(u_2)&D_1(u_1)D_1(u_2)
\end{array}
\right)
\end{equation}
これも前述の通り、$6$頂点模型の$A(u)$から$D(u)$の定義と$B(u)$と$C(u)$の位置が逆になっていることに注意しなければならない。また、$AB\neq BA$などにも注意を要する。
$T(u)$の一般化として、$1\times L+1$高次元スピン頂点模型に対応するモノドロミー行列を$T_L(u)$とする。すなわち、
\begin{equation}
T_L(u)=\left(
\begin{array}{cc}
A_L(u)&C_L(u)\\
B_L(u)&D_L(u)
\end{array}
\right)\in\mathrm{End}(W\otimes V_0\otimes\cdots\otimes V_L)
\end{equation}
である。これは下図のように図示できる。
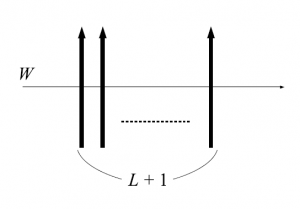
図50 $1\times L+1$高次元スピン頂点模型の略記図
この$T_L(u)$についても(12)と同じ式が成立して、
\begin{equation}
\check{X}(T_L(u_1)\otimes T_L(u_2))=(T_L(u_2)\otimes T_L(u_1))\check{X}\label{eq:5.3}
\end{equation}
である。
問題20
$6$頂点模型の(8)、(9)の導出を復習して、(13)が成立することを確かめよ。
解答20
一般化されたYang-Baxter 方程式より、今、
\[
X_{12}T_{L13}(u_1)T_{L23}(u_2)=T_{L23}(u_2)T_{L13}(u_1)X_{12}
\]
が成り立っている。これに左から$P_{12}$を掛けると、
\begin{align}
&P_{12}X_{12}T_{L13}(u_1)T_{L23}(u_2)=P_{12}T_{L23}(u_2)T_{L13}(u_1)X_{12}\nonumber\\
=&P_{12}T_{L23}(u_2)P_{12}P_{12}T_{L13}(u_1)P_{12}P_{12}X_{12}=T_{L13}(u_1)T_{L23}(u_2)P_{12}X_{12}\nonumber\\
\Longleftrightarrow&\check{X}_{12}T_{L13}(u_1)T_{L23}(u_2)=T_{L13}(u_1)T_{L23}(u_2)\check{X}_{12}\nonumber
\end{align}
となる。これにより、
\[
\check{X}(T_L(u_1)\otimes T_L(u_2))=(T_L(u_2)\otimes T_L(u_1))\check{X}
\]
と書くことが出来る。よって題意は示された。
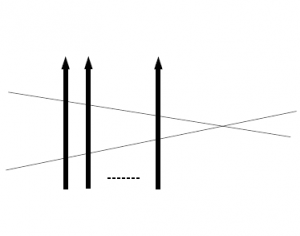
図51 $6$頂点模型の略記図
$=$
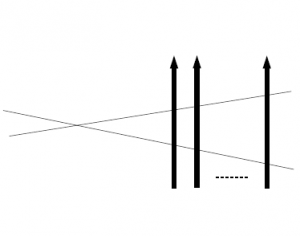
図52 $6$頂点模型の略記図
$6$頂点模型の(9)と同様、(13)から$A_L(u)$から$D_L(u)$についての関係式が以下のように得られる。
\begin{equation}
\left\{
\begin{array}{rcl}
A_L(u_1)A_L(u_2)&=&A_L(u_2)A_L(u_1)\\
B_L(u_1)B_L(u_2)&=&B_L(u_2)B_L(u_1)\\
D_L(u_1)D_L(u_2)&=&D_L(u_2)D_L(u_1)\\
B_L(u_1)D_L(u_2)&=&\dfrac{u_1-u_2}{qu_1-u_2}D_L(u_2)B_L(u_1)+\dfrac{(1-q)u_2}{u_2-qu_1}B_L(u_2)D_L(u_1)
\end{array}
\right.\label{eq:5.4}
\end{equation}
以上が高次元スピン頂点模型における可積分性からの帰結である。
問題21
(4)を確かめよ。
解答21
\[
\check{X}=\left(
\begin{array}{cccc}
u_1-qu_2&0&0&0\\
0&(1-q)u_2&u_1-u_2&0\\
0&q(u_1-u_2)&(1-q)u_1&0\\
0&0&0&u_1-qu_2
\end{array}
\right)
\]
であるから、与式に代入して両辺の各成分をあらわに書くと、
\begin{align}
&\check{X}(T_L(u_1)\otimes T_L(u_2))=\left(
\begin{array}{cccc}
u_1-qu_2&0&0&0\\
0&(1-q)u_2&u_1-u_2&0\\
0&q(u_1-u_2)&(1-q)u_1&0\\
0&0&0&u_1-qu_2
\end{array}
\right)\nonumber\\
& \left(
\begin{array}{rrrr}
A_L(u_1)A_L(u_2)&A_L(u_1)C_L(u_2)&C_L(u_1)A_L(u_2)&C_L(u_1)C_L(u_2)\\
A_L(u_1)B_L(u_2)&A_L(u_1)D_L(u_2)&C_L(u_1)B_L(u_2)&C_L(u_1)D_L(u_2)\\
B_L(u_1)A_L(u_2)&B_L(u_1)C_L(u_2)&D_L(u_1)A_L(u_2)&D_L(u_1)C_L(u_2)\\
B_L(u_1)B_L(u_2)&B_L(u_1)D_L(u_2)&D_L(u_1)B_L(u_2)&D_L(u_1)D_L(u_2)
\end{array}
\right)\nonumber\\
=&\small\left(
\begin{array}{cc}
A_L(u_1)A_L(u_2) (u_1-q u_2) & A_L(u_1)C_L(u_2) (u_1-q u_2)\\
B_L(u_1)A_L(u_2) (u_1-u_2)+A_L(u_1)B_L(u_2) (1-q) u_2 & B_L(u_1)C_L(u_2) (u_1-u_2)+A_L(u_1)D_L(u_2) (1-q) u_2\\
B_L(u_1)A_L(u_2) (1-q) u_1+A_L(u_1)B_L(u_2) q (u_1-u_2) & B_L(u_1)C_L(u_2) (1-q) u_1+A_L(u_1)D_L(u_2) q (u_1-u_2)\\
B_L(u_1)B_L(u_2) (u_1-q u_2) & B_L(u_1)D_L(u_2) (u_1-q u_2)
\end{array}
\right.\nonumber\\
&\small\left.
\begin{array}{cc}
C_L(u_1)A_L(u_2) (u_1-q u_2) & C_L(u_1)C_L(u_2) (u_1-q u_2) \\
D_L(u_1)A_L(u_2) (u_1-u_2)+C_L(u_1)B_L(u_2) (1-q) u_2 & D_L(u_1)C_L(u_2) (u_1-u_2)+C_L(u_1)D_L(u_2) (1-q) u_2 \\
D_L(u_1)A_L(u_2) (1-q) u_1+C_L(u_1)B_L(u_2) q (u_1-u_2) & D_L(u_1)C_L(u_2) (1-q) u_1+C_L(u_1)D_L(u_2) q (u_1-u_2) \\
D_L(u_1)B_L(u_2) (u_1-q u_2) & D_L(u_1)D_L(u_2) (u_1-q u_2)
\end{array}
\right)\nonumber
\end{align}
\begin{align}
&(T_L(u_2)\otimes T_L(u_1))\check{X}=\left(
\begin{array}{rrrr}
A_L(u_2)A_L(u_1)&A_L(u_2)C_L(u_1)&C_L(u_2)A_L(u_1)&C_L(u_2)C_L(u_1)\\
A_L(u_2)B_L(u_1)&A_L(u_2)D_L(u_1)&C_L(u_2)B_L(u_1)&C_L(u_2)D_L(u_1)\\
B_L(u_2)A_L(u_1)&B_L(u_2)C_L(u_1)&D_L(u_2)A_L(u_1)&D_L(u_2)C_L(u_1)\\
B_L(u_2)B_L(u_1)&B_L(u_2)D_L(u_1)&D_L(u_2)B_L(u_1)&D_L(u_2)D_L(u_1)
\end{array}
\right)\nonumber\\
& \left(
\begin{array}{cccc}
u_1-qu_2&0&0&0\\
0&(1-q)u_2&u_1-u_2&0\\
0&q(u_1-u_2)&(1-q)u_1&0\\
0&0&0&u_1-qu_2
\end{array}
\right)\nonumber\\
=&\left(
\begin{array}{cc}
A_L(u_2)A_L(u_1) (u_1-q u_2) & C_L(u_2)A_L(u_1) q (u_1-u_2)+A_L(u_2)C_L(u_1) (1-q) u_2 \\
A_L(u_2)B_L(u_1) (u_1-q u_2) & C_L(u_2)B_L(u_1) q (u_1-u_2)+A_L(u_2)D_L(u_1) (1-q) u_2 \\
B_L(u_2)A_L(u_1) (u_1-q u_2) & D_L(u_2)A_L(u_1) q (u_1-u_2)+B_L(u_2)C_L(u_1) (1-q) u_2 \\
B_L(u_2)B_L(u_1) (u_1-q u_2) & D_L(u_2)B_L(u_1) q (u_1-u_2)+B_L(u_2)D_L(u_1) (1-q) u_2
\end{array}
\right.\nonumber\\
& \left.
\begin{array}{cc}
C_L(u_2)A_L(u_1) (1-q) u_1+A_L(u_2)C_L(u_1) (u_1-u_2) & C_L(u_2)C_L(u_1) (u_1-q u_2) \\
C_L(u_2)B_L(u_1) (1-q) u_1+A_L(u_2)D_L(u_1) (u_1-u_2) & C_L(u_2)D_L(u_1) (u_1-q u_2) \\
D_L(u_2)A_L(u_1) (1-q) u_1+B_L(u_2)C_L(u_1) (u_1-u_2) & D_L(u_2)C_L(u_1) (u_1-q u_2) \\
D_L(u_2)B_L(u_1) (1-q) u_1+B_L(u_2)D_L(u_1) (u_1-u_2) & D_L(u_2)D_L(u_1) (u_1-q u_2)
\end{array}
\right)\nonumber
\end{align}
となる。$(1,1)$成分、$(1,4)$成分、$(4,4)$成分、$(2,4)$成分などを比較することで所望の式を得ることが出来る。よって題意は示された。