$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}
\def\Ket#1{{\left|{#1}\right\rangle}}$

前回の内容をランダムウォークなどに応用するために$L+1$のところで$L\rightarrow\infty$の極限を取りたいが、これは不都合が生じてしまう。この解決方法を考えてみよう。

高次元スピン頂点模型の分配関数と対称関数1

そこで今、signature を以下のように定義する。

\begin{equation}
\left\{
\begin{array}{lcl}
\mathrm{Sign}_N&=&\{\lambda=(\lambda_1,\cdots,\lambda_N)|\lambda_i\in\mathbb{Z},\lambda_1\geq\lambda_2\geq\cdots\lambda_N\}\\
&&\\
\mathrm{Sign}^+_N&=&\{\lambda=(\lambda_1,\cdots,\lambda_N)|\lambda_i\in\mathbb{Z},\lambda_1\geq\lambda_2\geq\cdots\lambda_N\geq0\}\\
&&\\
\mathrm{Sign}_0&=&\mathrm{Sign}^+_0\coloneqq\{\phi\}:\mathrm{empty~set}\\
&&\\
\mathrm{Sign}^+&=&\displaystyle\bigsqcup_{N\geq0}\mathrm{Sign}^+_N
\end{array}
\right.
\end{equation}

また、重複度を用いたあらわし方もある。$\mu\in\mathrm{Sign}^+$とすると、$m_0,m_1,m_2,\cdots$を用いて、$\mu=0^{m_0}1^{m_1}2^{m_2}\cdots$とあらわすことがある。但し、$m_j:\mu=(\mu_1,\mu_2,\cdots,\mu_N)$の中の$j$の出現回数である。例えば、

\begin{equation}
\mu=(4,4,4,3,3,2,2,2,2,2,1,1,0)
\end{equation}

であるとき、$\mu=(0^1,1^2,2^5,3^2,4^3)$である。

演算子$A$、$B$と対称関数$F_{\mu/\lambda}(u_1,\cdots,u_n)$、$G_{\mu/\lambda}(u_1,\cdots,u_n)$

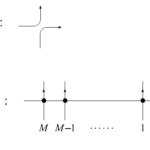
$V\coloneqq V_0\otimes V_1\otimes V_2\otimes\cdots$を$V_l=\{e_j\}_{j\geq0}$を基底とするベクトル空間であると定義する。また、分割$\mu\in\mathrm{Sign}^+$に対して、$e_\mu=e_{m_0}\otimes e_{m_1}\otimes e_{m_2}\otimes\cdots$として、$\bar{V}^{\mathrm{fin}}(\subset V):e_\mu$を$\mu\in\mathrm{Sign}^+$で張られる$V$の部分ベクトル空間であると定義する。

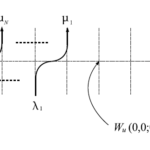
また、$A(u),B(u)\in\mathrm{End}(\bar{V}^{\mathrm{fin}})$を次のように定義する。$\lambda\in\mathrm{Sign}^+_N$、$N=0,1,2,\cdots$に対して、

\begin{equation}
\left\{
\begin{array}{lcr}
A(u)e_\lambda&=&\displaystyle\sum_{\mu\in\mathrm{Sign}^+_N}~\mathrm{Weight}(図53)e_\mu\\
&&\\
B(u)e_\lambda&=&\displaystyle\sum_{\mu\in\mathrm{Sign}^+_{N+1}}~\mathrm{Weight}(図54)e_\mu
\end{array}
\right.
\end{equation}
となる。但し、上のWeight は$L>\mu_1$として、$1\times L$の高次元スピン模型のWeight である。$L>\mu_1$を満たせば、どこで$L$を取ってもWeight は$L$に依らず同じ値となる。このとき、$G_{\mu/\lambda}(u)$と$F_{\mu/\lambda}(u)$をそれぞれ以下のように定義する。

\begin{equation}
\left\{
\begin{array}{lcr}
G_{\mu/\lambda}(u)&=&\mathrm{Weight}(図53)e_\mu\\
&&\\
F_{\mu/\lambda}(u)&=&\mathrm{Weight}(図54)e_\mu
\end{array}
\right.
\end{equation}

$A(u)$は横から粒子が入ってこないのに対して、$B(u)$は横から粒子が$1$つだけ入ってくるという違いがある。出ていくときはいずれも上だけに出て行き、右に出ていくことはない。

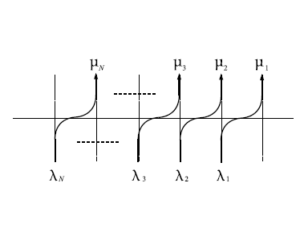
図53 $6$頂点模型の略記図

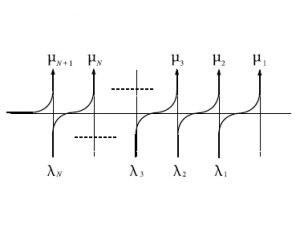
図54 $6$頂点模型の略記図

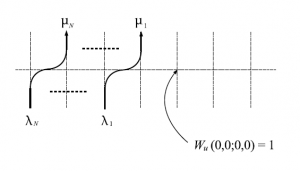
図55 高次元スピン頂点模型の略記図

更に、$F_{\mu/\lambda}(u_1,\cdots,u_n)$と$G_{\mu/\lambda}(u_1,\cdots,u_n)$を以下のように定義する。

\begin{equation}
\left\{
\begin{array}{lcr}
A(u_1)\cdots A(u_n)e_\lambda&=&\displaystyle\sum_{\mu\in\mathrm{Sign}^+_N}G_{\mu/\lambda}(u_1,\cdots,u_n)e_\mu\\
&&\\
B(u_1)\cdots B(u_n)e_\lambda&=&\displaystyle\sum_{\mu\in\mathrm{Sign}^+_{N+n}}F_{\mu/\lambda}(u_1,\cdots,u_n)e_\mu
\end{array}
\right.
\end{equation}

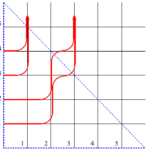
但し、$\lambda\in\mathrm{Sign}^+_N$である。この定義から分かるように、対称関数$F_{\mu/\lambda}(u_1,\cdots,u_n)$、$G_{\mu/\lambda}(u_1,\cdots,u_n)$は$n\times”\infty”$の正方格子上の高次元スピン模型の分配関数になっている。

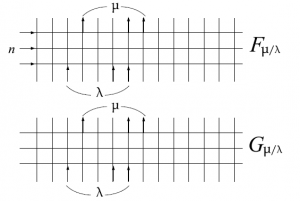
図56 高次元スピン頂点模型の略記図

$F_{\mu/\lambda}(u_1,\cdots,u_n)$と$G_{\mu/\lambda}(u_1,\cdots,u_n)$の性質

$F_{\mu/\lambda}(u_1,\cdots,u_n)$と$F_{\mu/\lambda}(u_1,\cdots,u_n)$にはそれぞれ以下のような性質がある。

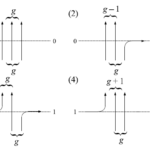
(1)$F_{\mu/\lambda}(u_1,\cdots,u_n)$と$F_{\mu/\lambda}(u_1,\cdots,u_n)$はどちらも$u_i,u_j~(i\neq j)$の入れ替えについて対称である。

(2)$\mu\in\mathrm{Sign}^+_{N+n_1+n_2}$、$\lambda\in\mathrm{Sign}^+_N$について以下が成り立つ。

\begin{equation}
F_{\mu/\lambda}(u_1,\cdots,u_{n_1+n_2})=\sum_{\kappa\in\mathrm{Sign}^+_{N+n_1}}F_{\mu/\kappa}(u_{n_1+1},\cdots,u_{n_1+n_2})F_{\kappa/\lambda}(u_1,\cdots,u_{n_1})
\end{equation}

(3)$\mu\in\mathrm{Sign}^+_N$、$\lambda\in\mathrm{Sign}^+_N$について以下が成り立つ。

\begin{equation}
G_{\mu/\lambda}(u_1,\cdots,u_{n_1+n_2})=\sum_{\kappa\in\mathrm{Sign}^+_N}G_{\mu/\kappa}(u_{n_1+1},\cdots,u_{n_1+n_2})G_{\kappa/\lambda}(u_1,\cdots,u_{n_1})
\end{equation}

なお、量子可積分系におけるSchur 関数やMacdonald 多項式も対称関数であり、これらの性質を満たすことが知られている。

問題22

性質(1)～(3)を確かめよ。

解答22

前回の問題で確認したように$A(u_i),B(u_i)~(i=1,\cdots,n)$は可換であるから、性質(1)は自明。
性質(2)、(3)は$F_{\mu/\lambda}(u_1,\cdots,u_n)$と$G_{\mu/\lambda}(u_1,\cdots,u_n)$の定義、

\begin{equation}
\left\{
\begin{array}{lcr}
A(u_1)\cdots A(u_n)e_\lambda&=&\displaystyle\sum_{\mu\in\mathrm{Sign}^+_N}G_{\mu/\lambda}(u_1,\cdots,u_n)e_\mu\\
&&\\
B(u_1)\cdots B(u_n)e_\lambda&=&\displaystyle\sum_{\mu\in\mathrm{Sign}^+_{N+n}}F_{\mu/\lambda}(u_1,\cdots,u_n)e_\mu
\end{array}
\right.
\end{equation}

から直ちに得られる。