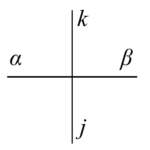$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}
\def\Ket#1{{\left|{#1}\right\rangle}}$
確率的頂点模型
以下では、$0<q<1$、$-1<s<0$、$u_i\geq0$、$v_i\geq0 (i=1,2,\cdots)$という制限を与える。このとき、ウェイト$W_{u_i}$、$W_{v_i}$、$W^c_{u_i}$、$W^c_{v_i}$、$L_{u_i}$は非負となる。また、$(u_i,v_j)\in\mathrm{Adm}$は依然として課しているとする。
$\mathrm{Sign}^+$上のMarkov 連鎖
$\nu\in\mathrm{Sign}^+_M$、$\bm{u}=(u_1,u_2,\cdots,u_M)$、$\bm{v}=(v_1,v_2,\cdots,v_N)$として$\nu$の確率測度を以下のように導入する。
\begin{equation}
M_{\bm{u}:\bm{v}}(\nu)\coloneqq\dfrac{1}{Z(\bm{u}:\bm{v})}F_\nu(u_1,\cdot,u_M)G^c_\nu(v_1,\cdots,v_N)\tag{1}
\end{equation}
但し、
\begin{equation}
Z(\bm{u}:\bm{v})=(q:q)_M\prod_{i=1}^M\left(\dfrac{1}{1-su_i}\prod_{j=1}^N\dfrac{1-qu_iv_j}{1-u_iv_j}\right)
\end{equation}
前回の(8)より、$M_{\bm{u}:\bm{v}}(\nu)$は確かに$\mathrm{Sign}^+_M$上の確率測度になっていることあが分かる。また、特に以下の式が成り立つことに注意せよ。但し、$\phi$は$M=0$であることを意味する。
\begin{equation}
M_{\phi:\bm{v}}(\nu)=\delta_{\nu,\phi} , M_{\bm{u}:\phi}(\nu)=\delta_{\nu,0^M}
\end{equation}
更に、$\lambda\in\mathrm{Sign}^+_m$から$\nu\in\mathrm{Sign}^+_{m+1}$への確率的な成長を記述するものとして、
\begin{equation}
Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)\coloneqq\dfrac{1-su}{1-q^{m+1}}\left(\prod_{j=1}^N\dfrac{1-uv_j}{1-quv_j}\right)\dfrac{G^c_\nu(v_1,\cdots,v_N)}{G^c_\lambda(v_1,\cdots,v_N)}F_{\nu/\lambda}(u)\tag{2}
\end{equation}
を導入する。このとき、$Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)$はMarkov 核になっていること、すなわち、
\begin{equation}
\left\{
\begin{array}{rcl}
Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)&\geq&0\\
&&\\
\displaystyle\sum_{\nu\in\mathrm{Sign}^+_{m+1}}Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)&=&1
\end{array}
\right.\tag{3}
\end{equation}
であることに注意せよ。
問題24
(3)を確かめよ。
解答24
前回の記事で扱った関係式、
\[
\sum_{\kappa\in\mathrm{Sign}^+_{N+1}}G^c_{\kappa}(v_1,\cdots,v_n)F_{\kappa/\nu}(u)=\dfrac{1-q^{N+1}}{1-su}\prod_{j=1}^n\dfrac{1-quv_j}{1-uv_j}G^c_\nu(v_1,\cdots,v_n)
\]
を利用して式変形を行うと、
\begin{align}
&\displaystyle\sum_{\nu\in\mathrm{Sign}^+_{m+1}}Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)=\dfrac{1-su}{1-q^{m+1}}\left(\prod_{j=1}^N\dfrac{1-uv_j}{1-quv_j}\right)\dfrac{1}{G^c_\lambda(v_1,\cdots,v_N)}\sum_{\nu\in\mathrm{Sign}^+_{m+1}}G^c_\nu(v_1,\cdots,v_N)F_{\nu/\lambda}(u)\nonumber\\
=&\dfrac{1-su}{1-q^{m+1}}\left(\prod_{j=1}^N\dfrac{1-uv_j}{1-quv_j}\right)\dfrac{1}{G^c_\lambda(v_1,\cdots,v_N)}\times\dfrac{1-q^{m+1}}{1-su}\prod_{j=1}^N\dfrac{1-quv_j}{1-uv_j}G^c_\lambda(v_1,\cdots,v_N)=1\nonumber
\end{align}
となる。よって題意は示された。
上の$M_{\bm{u}:\bm{v}}(\lambda)$と$Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)$は以下の式を満たす。
\begin{equation}
\sum_{\in\mathrm{Sign}^+_m}M_{\bm{u}:\bm{v}}(\lambda)Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)\tag{4}
\end{equation}
但し、$\lambda\in\mathrm{Sign}^+_m$と$\nu\in\mathrm{Sign}^+_{m+1}$であることに注意せよ。
問題25
(4)を確かめよ。
解答25
\begin{align}
&\displaystyle\sum_{\lambda\in\mathrm{Sign}^+_m}M_{\bm{u}:\bm{v}}(\lambda)Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)=\sum_{\lambda\in\mathrm{Sign}^+_m}\dfrac{1}{Z(\bm{u}:\bm{v})}F_\lambda(u_1,\cdots,u_M)G^c_\lambda(v_1,\cdots,v_N)\nonumber\\
&\times\dfrac{1-su}{1-q^{m+1}}\left(\prod_{j=1}^N\dfrac{1-uv_j}{1-quv_j}\right)\dfrac{G^c_\nu(v_1,\cdots,v_N)}{G^c_\lambda(v_1,\cdots,v_N)}F_{\nu/\lambda}(u)=M_{\bm{u}\cup u,\bm{v}}(\nu)\nonumber
\end{align}
よって題意は示された。
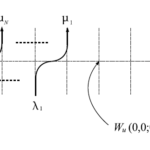
さて、$Q^+_{u:\bm{v}}(\lambda\rightarrow\nu)$によるMarkov 連鎖的な成長過程を考えたい。$\lambda^{(j)}$を$\mathrm{Sign}^+_j$に値を持つ確率変数、
\begin{equation}
\lambda^{(0)}=\phi\overset{Q^+_{u_1:\bm{v}}}{\longrightarrow}\lambda^{(1)}\overset{Q^+_{u_2:\bm{v}}}{\longrightarrow}\lambda^{(2)}\overset{Q^+_{u_3:\bm{v}}}{\longrightarrow}\cdots\overset{Q^+_{u_M:\bm{v}}}{\longrightarrow}\lambda^{(M)}
\end{equation}
として、
\begin{equation}
P(\lambda^{(M)}=\nu|\lambda^{(0)}=\phi)=\bigl(M_{\phi:\bm{v}}Q^+_{u_1:\bm{v}}Q^+_{u_2:\bm{v}}\cdots Q^+_{u_M:\bm{v}}\bigr)(\nu)\overset{(\ref{eq:7.4})}{=}M_{\bm{u}:\bm{v}}(\nu)\tag{5}
\end{equation}
パラメーター$\bm{v}$の特殊化と確率的頂点模型
これまでの議論から確率頂点模型を出すことを考えたい。
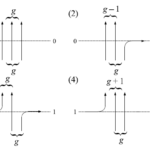
| $W_u(i_1,j_1;i_2,j_2)$ | $(1)$ | $(2)$ | $(3)$ | $(4)$ |
| $W_u(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{(1-s^2q^{g-1})u}{1-su}$ | $\dfrac{u-sq^g}{1-su}$ | $\dfrac{1-q^{g+1}}{1-su}$ |
| $W_u^c(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{(1-q^g)u}{1-su}$ | $\dfrac{u-sq^g}{1-su}$ | $\dfrac{1-s^2q^g}{1-su}$ |
| $L_u(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{-su(1-q^g)}{1-su}$ | $\dfrac{-s(u-sq^g)}{1-su}$ | $\dfrac{1-s^2q^g}{1-su}$ |
表2 Yang-Baxter 方程式
$3$つのウェイトの関係は以下のようになる。
\begin{equation}
\left\{
\begin{array}{rcl}
W^c_u(i_1,j_1;i_2,j_2)&=&\dfrac{(s^2:q)_{i_2}}{(q:q)_{i_2}}\dfrac{(q:q)_{i_1}}{(s^2:q)_{i_1}}W_u(i_1,j_1;i_2,j_2)\\
&&\\
L_u(i_1,j_1;i_2,j_2)&=&(-1)^{j_2}W^c_u(i_1,j_1;i_2,j_2)
\end{array}
\right.\tag{6}
\end{equation}
まとめると、以下の表のようになる。
| 各頂点のウェイト | 上の図の配置における分配関数 |
| $W_u$ | $F_{\mu/\lambda}(u)$ |
| $W^c_u$ | $F^c_{\mu/\lambda}(u)\coloneqq\dfrac{c(\mu)}{c(\lambda)}F_{\mu/\lambda}(u)$ |
| $L_u$ | $(-1)^{|\mu|-|\lambda|}F^c_{\mu/\lambda}(u)$ |
表3 各頂点のウェイトと分配関数の関係
但し、上の表ではそれぞれ
\begin{equation}
c(\mu)=\prod_k\dfrac{(s^2:q)_{n_k}}{(q:q)_{n_k}} , \mu=0^{n_0}1^{n_1}2^{n_2}\cdots , |\mu|=\mu_1+\mu_2+\cdots
\end{equation}
という定義になっている。一方、(2)は
\begin{equation}
Q^+_{u:\bm{v}}(\lambda\rightarrow\mu)=\dfrac{1-su}{1-s^2q^m}\left(\prod_{j=1}^N\dfrac{1-uv_j}{1-quv_j}\right)\dfrac{G_\mu(v_1,\cdots,v_N)}{G_\lambda(v_1,\cdots,v_N)}F^c_{\mu/\lambda}(u)\tag{8}
\end{equation}
但し、以下のことに注意せよ。
\begin{equation}
G^c_\mu=\dfrac{c(\mu)}{c(0^m)}G_\mu , \mu\in\mathrm{Sign}_m^+
\end{equation}
次に、(8)のパラメーター$\bm{v}$を特殊化することで表3の形に持っていくことを考える。
パラメーター$\bm{v}$の特殊化:$\rho$
$v_1,\cdots,v_N$の関数$f(v_1,\cdots,v_N)$を用いて、
\begin{equation}
f(\rho)\coloneqq\lim_{\varepsilon\rightarrow0}\left(\biggl.f(\varepsilon,q\varepsilon,\cdots,q^{N-1}\varepsilon)\biggr|_{q^N=1/(s\varepsilon)}\right)
\end{equation}
を導入する。これは、$f(\varepsilon,q\varepsilon,\cdots,q^{N-1}\varepsilon)$を変数$q^N$の関数とみなして、$q^N$を$1/(s\varepsilon)$へと解析接続するということを意味している。
例えば、関数$f(v_1,\cdots,v_N)$が
\begin{equation}
f(v_1,\cdots,v_N)=\prod_{j=1}^N\dfrac{1-uv_j}{1-quv_j}
\end{equation}
であれば、$f(\varepsilon,q\varepsilon,\cdots,q^{N-1}\varepsilon)$は次の式で与えられる。
\begin{equation}
f(\varepsilon,q\varepsilon,\cdots,q^{N-1}\varepsilon)=\dfrac{1-u\varepsilon}{1-qu\varepsilon}\dfrac{1-qu\varepsilon}{1-q^2u\varepsilon}\cdots\dfrac{1-q^{N-1}u\varepsilon}{1-q^Nu\varepsilon}=\dfrac{1-u\varepsilon}{1-q^Nu\varepsilon}\overset{q^N=1/(s\varepsilon)}{\longrightarrow}\dfrac{1-u\varepsilon}{1-\dfrac{u}{s}}
\end{equation}
つまり、
\begin{equation}
f(\rho)=\dfrac{1}{1-\dfrac{u}{s}}\tag{9}
\end{equation}
となる。数学的には、このような解析接続はいつも行えるわけではない。しかし、この議論では問題にならないのでこの点については言及しない。また、$\nu\in\mathrm{Sign}^+_n$を用いて
\begin{equation}
G_\nu(\rho)=\left\{
\begin{array}{ccl}
(-s)^{|\nu|}(s^2:q)_ns^{-2n}&\mathrm{if}&\nu_n>0\\
&&\\
0&\mathrm{if}&\nu_n=0
\end{array}
\right.\tag{10}
\end{equation}
が成り立つ。特に、$(-s)^{|\nu|}$の部分は表3の$(-1)^{|\mu|-|\lambda|}$が反映されていることに注意せよ。(9)、(10)を用いると、以下の$2$つの事実が分かる。
- $\nu\in\mathrm{Sign}^+_{m+1},\lambda\in\mathrm{Sign}^+_m~\mathrm{such~that}~\nu_{m+1}>0,\lambda_m>0$に対して、
\begin{equation}
Q^+_{u:\rho}(\lambda\rightarrow\nu)=(-s)^{|\tilde{\nu}|-|\tilde{\lambda}|}F^c_{\tilde{\nu}/\tilde{\lambda}}\tag{11}
\end{equation}
但し、
\begin{equation}
\tilde{\nu}=\nu-\overbrace{(1,1,\cdots,1)}_{m+1} , \tilde{\lambda}=\lambda-\overbrace{(1,1,\cdots,1)}_{m+1}
\end{equation}
- \item $\nu\in\mathrm{Sign}^+_M$に対して、
\begin{equation}
M_{\bm{u}:\rho}(\nu)=\dfrac{1}{Z(\bm{u}:\rho)}F_\nu(u_1,\cdots,u_M)G^c_\nu(\rho)=1_{\nu_n\geq1}(-s)^{|\tilde{\nu}|}F^c_{\tilde{\nu}}(u_1,\cdots,u_M)\tag{12}
\end{equation}
従って、(5)、表3、(11)より、$M_{\bm{u}:\rho}$の式(12)は確率的頂点模型の$M$段目の配置が$\nu=1^{n_1}2^{n_2}\cdots$であるような確率を与えると解釈出来る。