$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\rmd}{\mathrm{d}}$

第12講の導入

今回は万有引力の下での惑星の運動、いわゆるケプラー問題について考えてみましょう。歴史的には、ニュートンはケプラーの法則などを基にしてニュートンの万有引力とニュートンの運動法則を見出しました。ここでは、その逆を辿り、ニュートンの万有引力の法則とニュートンの運動法則からケプラーの法則が導くことを目指してお話を進めて行きます。

中心力問題の運動は平面内に限られるということ

質量$m$の惑星（例えば地球など）が質量$M$の太陽の周りを回っている状況を考えてみましょう。ニュートンの万有引力の法則によれば、惑星は太陽に向かう方向に、以下の式で与えられるような距離の$2$乗に反比例した力$F$を受けています。
\[
F = – m \frac { H } { r ^ { 2 } }
\]
但し、$H$は$H=GM$という定数です。今、太陽の質量は惑星の質量よりも十分大きい（$M\gg m$）ということを考えると、太陽は近似的に動かないとみなすことが出来ます。そこで、太陽を座標系の原点を取れば、この力は中心力であるとみなせるため、原点のまわりの角運動量が保存され、惑星の運動は質点の速度ベクトルと原点を含むような平面内で留まり続けることになります。このことは、第07講で扱いましたので、忘れてしまっている人はそこの項目を復習してください。以下ではそのような平面内に限定して惑星運動を論じることにします。

軌道の方程式を解くこと

さて、惑星に生じる加速度を平面極座標成分に分けて
\[
\boldsymbol { a } = a _ { r } \boldsymbol { e } _ { r } + a _ { \theta } \boldsymbol { e } _ { \theta }
\]
とあらわすと、引力が中心力であることから$\theta$成分の加速度は$0$となる必要があります。すなわち、
\[
a _ { \theta } = r \ddot { \theta } + 2 \dot { r } \dot { \theta } = \frac { 1 } { r } \frac { d } { d t } \left( r ^ { 2 } \dot { \theta } \right) = 0
\]
となります。ここで角運動量$L=mr^2\dot{\theta}$は変化しないので、$L$を定数であると考えて、
\[
\dot { \theta } = \frac { L } { m r ^ { 2 } }
\]
と書くことが出来ます。これはケプラーの第2法則、すなわち面積速度一定の法則に対応しています。これを動径方向の運動方程式に代入すると、
\[
– \frac { H } { r ^ { 2 } } = a _ { r } = \ddot { r } – r \dot { \theta } ^ { 2 }= \frac { d ^ { 2 } r } { d t ^ { 2 } } – \frac { L ^ { 2 } } { m ^ { 2 } r ^ { 3 } }
\]
となります。これは距離$r$の時間$t$に関する常微分方程式ですから、これを解くとその時間変化を追うことが出来ます。しかし、ここでは距離の時間依存性を直接見るのではなく、軌道の方程式を出したいので、距離$r$を時間$t$ではなく角度$\theta$についての常微分方程式に書き直すことを考えることになります。

まず、時間に関する$1$階微分は合成関数の微分の関係式を利用して
\[
\dot { r } = \frac { d r } { d t } = \frac { d \theta } { d t } \frac { d r } { d \theta } = \frac { L } { m r ^ { 2 } } \frac { d r } { d \theta } = – \frac { L } { m } \frac { d } { d \theta } \left( \frac { 1 } { r } \right)
\]
と書くことが出来ます。同様に、時間に関する$2$階微分は
\[
\ddot { r } = \frac { d } { d t } \dot { r } = \frac { d \theta } { d t } \frac { d } { d \theta } \dot { r }= \frac { L } { m r ^ { 2 } } \frac { d } { d \theta } \dot { r } = – \frac { L ^ { 2 } } { m ^ { 2 } r ^ { 2 } } \frac { d } { d \theta } \frac { d } { d \theta } \left( \frac { 1 } { r } \right)
\]
となります。これを先ほどの常微分方程式に代入すると、
\[
– \frac { L ^ { 2 } } { m ^ { 2 } } \left\{ \frac { 1 } { r ^ { 2 } } \frac { d ^ { 2 } } { d \theta ^ { 2 } } \left( \frac { 1 } { r } \right) + \frac { 1 } { r ^ { 3 } } \right\} = – H \frac { 1 } { r ^ { 2 } }
\]
が得られます。これを解きやすくするために、両辺に$-(mr/L)^2$を掛けて$u=1/r$とおくと、
\[
\frac { d ^ { 2 } u } { d \theta ^ { 2 } } + u = \frac { H m ^ { 2 } } { L ^ { 2 } }
\]
となります。これで、太陽からの距離$r$の時間に対する依存性をあらわす常微分方程式は、距離の逆数$u$の角度に対する依存性をあらわす常微分方程式へと書き換えられました。これを解くと、
\[
u = \frac { H m ^ { 2 } } { L ^ { 2 } } + A \cos (\theta+\delta)= \frac { H m ^ { 2 } } { L ^ { 2 } } + A \cos \theta
\]
となります。但し、途中で、初期位相$\delta$は座標系を見ているだけの文字なので、$\delta=0$としても一般性を失わないとして$0$と採りました。これを$r$の戻すと、
\[
r = \frac { 1 } { H m ^ { 2 } / L ^ { 2 } + A \cos \theta } = \frac { L ^ { 2 } / \left( H m ^ { 2 } \right) } { 1 + A L ^ { 2 } / \left( H m ^ { 2 } \right) \cos \theta }
\]
と書くことが出来ます。

第12講のまとめ

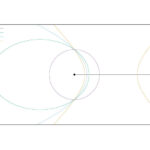
最後に一言コメントをして第12講を終わりにしましょう。ここで求めた軌道の式は$\left| A L ^ { 2 } / \left( H m ^ { 2 } \right) \right|$の値によって異なる曲線を表すことになります。これがケプラーの第1法則と関連することになります。特に軌道を楕円軌道と限定することでケプラーの第3法則も導くことが出来ます。これらの解説を次回の記事で行いたいと思います。