$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\rmd}{\mathrm{d}}$

第13講の導入

今回は、前回に引き続いてケプラー問題について考えていきましょう。前回、軌道の式
\[
r = \frac { L ^ { 2 } / \left( H m ^ { 2 } \right) } { 1 + A L ^ { 2 } / \left( H m ^ { 2 } \right) \cos \theta }
\]
を出したので、それについての場合分けから行っていきます。

楕円軌道とケプラーの第3法則

$\left| A L ^ { 2 } / \left( H m ^ { 2 } \right) \right|<1$のとき、考えている軌道は楕円軌道になります。従って、ニュートンの万有引力の法則とニュートンの運動法則を組み合わせることで、ケプラーの第1法則を導くことが出来ることになります。

これを楕円の極座標表示の標準形
\[
r = \frac { a \left( 1 – \varepsilon ^ { 2 } \right) } { 1 + \varepsilon \cos \theta }
\]
にあてはめると、この軌道の離心率は
\[
\varepsilon = \frac { A L ^ { 2 } } { H m ^ { 2 } }
\]
となり、長半径$a$は
\[
a \left( 1 – \varepsilon ^ { 2 } \right) = \frac { L ^ { 2 } } { H m ^ { 2 } }
\]
となります。

角運動量$L$を用いたときの面積速度$v_S$は、楕円の面積$S$を周期$T$で割ったものに等しいから、
\[
v _ { S } = \frac { L } { 2 m } = \frac { S } { T }
\]
が成り立ちます。従って、周期$T$の$2$乗は
\[
T ^ { 2 } = \left( \frac { 2 m } { L } \right) ^ { 2 } S ^ { 2 }
\]
で与えられます。楕円の面積は$S = \pi a b = \pi a ^ { 2 } \sqrt { 1 – \varepsilon ^ { 2 } }$で与えられるので、これを代入すると
\[
T ^ { 2 } = \left( \frac { 2 m } { L } \right) ^ { 2 } \pi ^ { 2 } a ^ { 4 } \left( 1 – \varepsilon ^ { 2 } \right)=\frac { 4 \pi ^ { 2 } a ^ { 3 } } { H }
\]
となります。これでケプラーの第3法則を導けました。

双曲線軌道と放物線軌道

ところで、軌道の式は$\left| A L ^ { 2 } / \left( H m ^ { 2 } \right) \right|>1$を満たすときには角度$\theta$に禁止領域が生じ、軌道は双曲軌道になります。これを双曲線の極座標表示の標準形
\[
r = \frac { a \left( \varepsilon ^ { 2 } – 1 \right) } { 1 – \varepsilon \cos \theta }
\]
にあてはめると、距離の差$2a$は$2$定点間の距離$2a\varepsilon$よりも大きく離れないため、$\varepsilon>1$となります。よって、角度は
\[
1 – \varepsilon \cos \theta > 0
\]
を満たすような範囲でなければならないことになります。ちなみに、先の解をこれに対応させると、$\varepsilon = – A L ^ { 2 } / \left( H m ^ { 2 } \right)$、$a \left( \varepsilon ^ { 2 } – 1 \right) = L ^ { 2 } / \left( H m ^ { 2 } \right)$となります。

この双曲線の議論はケプラーの法則にはありませんでした。双曲線軌道や放物線軌道を描く天体は太陽系に留まることがないので本来惑星という定義にはなりませんが、彗星には楕円軌道を描いて周期的に周回するものもあれば、放物線軌道や双曲線軌道をとって立ち去っていくものもあることが観測されています。

各軌道のまとめ

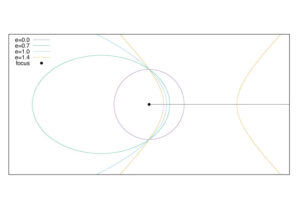
ここまでの議論を1つの図で書くと、次のようになります。それぞれ円軌道、楕円軌道、双曲線軌道、放物線軌道になっていることを確認してみてください。

第13講のまとめ

最後に一言コメントをして第13講を終わりにしましょう。第12講と第13講ではケプラー問題を例にして中心力が働く系の運動を論じました。他にも中心力が働く系は存在していて、例えばクーロン力による粒子散乱を古典力学の範囲で考える場合も中心力問題になります。これはラザフォード散乱と呼ばれていて、古典力学と量子力学の関係を理解するための重要な例の1つになっています。