$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\rmd}{\mathrm{d}}$

第14講の導入

第14講と第15講では、非慣性系（加速度系）における運動を論じることにします。非慣性系では慣性力と呼ばれる見かけの力が現れることになります。そして回転系では慣性力として遠心力とコリオリ力が現れます。これらについて、2回に分けて論じることにします．

相対運動と慣性力

今まで議論してきたように、一定の速度で動く座標系を慣性系と呼び、$2$つの慣性系の座標返還をガリレイ変換と呼びます。任意の慣性形で同じニュートンの運動方程式が成り立つことが分かります。例えば、一定の速度$v_0$で走っている電車に乗っている人が電車の中で物体を下に落下させると、
$$x = x _ { 0 } , z = z _ { 0 } – ( 1 / 2 ) g t ^ { 2 }$$
のように直線運動をします。一方で、この現象を地上、すなわち静止系で観測すると、
$$x = x _ { 0 } + v t , z = z _ { 0 } – ( 1 / 2 ) g t ^ { 2 }$$
のような放物運動になります。これらを比較すると、位置と速度は異なりますが、加速度はどちらの系でも$a_z=-g$となり、力も$-mg$で変わらないということが分かります。

これに対して、加速する電車やエレベーターなどのように、加速度$\bm{a}_0$で加速する座標系では加速度は次の式のように変換されます。
$$\boldsymbol { a } = \boldsymbol { a } ^ { \prime } + \boldsymbol { a } _ { 0 }$$
但し、$\bm{a}$は静止系の加速度、$\bm{a}’$は加速度系での加速度をあらわします。静止系での運動方程式$m\bm{a}=\bm{F}$にこれを代入すると、
$$m \boldsymbol { a } ^ { \prime } = \boldsymbol { F } – m \boldsymbol { a } _ { 0 }$$
となり、右辺には見かけの力$-m\bm{a}_0$、すなわち慣性力が現れます。このような加速する系を非慣性系といいます。非慣性系での時間変化を$d’/dt$であらわすことにすると、非慣性系での運動方程式は
$$m \frac { d ^ { \prime 2 } \boldsymbol { r } } { d t ^ { 2 } } = \boldsymbol { F } – m \boldsymbol { a } _ { 0 }$$
となります。

例えば、飛行機が離陸するときは斜め前向きに大きな加速度が生じます。このとき、飛行機に乗っている人には斜め後ろ向きの力$-m\bm{a}_0$がはたらき、座席に押し付けられるように感じます。

遠心力

次に、回転系について考えてみましょう。ここでいう回転系とは、角速度$\omega$で回転している系のことを指します。回転系では遠心力とコリオリ力という$2$種類の慣性力が現れることになります。

静止系から見て、角速度$\omega$、半径$r$の円運動をしている質量$m$の質点には$mr\omega^2$の中心力が働いています。この運動を角速度$\omega$で回転する座標系から見ると、質点は原点から$r$の距離の位置で静止しています。回転座標系では、中心力とつり合う外向きで大きさが$mr\omega^2$の力がはたらいていなければならないことになります。この慣性力を遠心力と呼びます。遠心力は回転座標系という加速度系に現れる見かけの力です。

例えば、車に乗ってカーブを曲がる時、車に乗っている人には外向きに遠心力$mr\omega^2=mv^2/r$が働きます。ここで、$r$はカーブの曲率半径、$v$は車の速度をあらわします。曲率半径$r$が小さいような急カーブでは大きな遠心力がはたらいてしまい、カーブを曲がり切れなくなるので、安全に運転するためには速度$v$を落として遠心力を下げる必要があります。このため、高速道路では道路の曲率半径の標識が出ていることがあります。

コリオリ力

回転系で動いている物体には遠心力に加えてコリオリ力という力もはたらきます。これはこの力を最初に導いた人の名前にちなんでいます。コリオリ力は遠心力に比べてややイメージが湧きづらいです。数学的な導出は次回に回すことにして、ここでは直観的な説明を行うことにします。

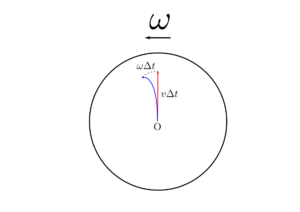
図のように、原点から一定の速度$\bm{v}=(v_x,v_y)$で進む質点を考察します。静止系では、質点は微小時間$\Delta t$の間に$\bm{r}=(v_x\Delta t,v_y\Delta t)=\bm{v}\Delta t$の位置まで直進します（赤線）。

一方で、これを角速度$\omega>0$、すなわち反時計回りに回転する円盤に乗った系から観測すると、$\Delta t$の間に円盤は角度$\omega\Delta t$だけ反時計回りに回転するので、回転系では質点は直進するのではなく、時計回り方向に角度が$\Delta\theta=\omega\Delta t$だけずれていくように見えます。原点からの距離は$\Delta r=|\bm{v}|\Delta t$なので、回転系の直進運動から$\Delta r\Delta \theta=\omega|\bm{v}|\Delta t^2$だけ右方向にずれていきます（青線）。時間とともに$\Delta t^2$で変異が生じるため、回転系では右向きに加速度$a$が生じて$(1/2)a\Delta t^2$だけずれたように見えるのです。すなわち、回転系では$ma=2m\omega|\bm{v}|$の慣性力がはたらいたと解釈します。力の方向は速度ベクトルに垂直右方向になるので、慣性力をベクトル表示すると$(2m\omega v_y,-2m\omega v_x)$となります。この慣性力をコリオリ力と呼びます。角速度ベクトルを$\bm{\omega}=(0,0,\omega)$とすると、コリオリ力はベクトル積の形$2m\bm{v}\times\bm{\omega}$で表すことが出来ます。

第14講のまとめ

最後に一言コメントをして第14講を終わりにしましょう。最後に考えたコリオリ力は、地球規模の大気の流れや海流にも影響を与えることが知られています。例えば、北半球の赤道付近ではコリオリ力によって東よりの貿易風が吹き、中緯度付近では偏西風が形成されます。その大規模な風により海水が駆動され、海流が生じることになります。

また、海流の流れもコリオリ力の影響を受けます。コリオリ力は$\Omega\sin{\phi}$に比例するので、緯度$\phi$が高くなるほど強くなります。緯度によるコリオリ力の変化により太平洋や大西洋の西側（ユーラシア大陸やアメリカ大陸の東側）で海流が強くなります。黒潮やメキシコ湾流などの大陸の東側を流れる海流が強くなるのはコリオリの力によって説明が出来るのです。このように、ボールや箱など日常の物体のスケールから地球規模まで同じ理論で考えることが出来るということからも、古典力学がいかに強力なものであるかを垣間見ることが出来ます。