$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\rmd}{\mathrm{d}}$

第15講の導入

第15講では前回に引き続き非慣性系の運動を考えることにします。今回は、より一般的に回転座標系での運動方程式を導出することを目標にして話を進めて行きます。

回転座標系での運動方程式

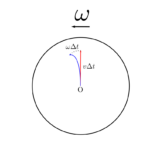
静止系を$S$とし、原点O を通る軸の周りで角速度$\omega$で回転している系を$S’$とします。大きさが$\omega$でこの回転軸の方向を向いたベクトルを角速度ベクトル$\bm{\omega}$であらわすことにします。回転系$S’$で止まっているベクトル$\bm{B}$は静止系では軸のまわりで角速度$\omega$で回転します。

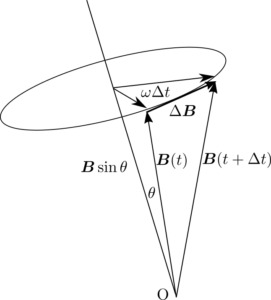
図のようにベクトル$\bm{B}$と回転軸のなす角を$\theta$とすると、微小時間$\Delta t$の間に$|\Delta\bm{B}|=|\bm{B}|\sin{\omega\Delta t}$だけベクトル$\bm{B}$が変化します。ベクトルの変化の方向は回転軸および$\bm{B}$の垂直方向なので、ベクトル$\bm{B}$の静止系での時間変化は
$$\frac { d \boldsymbol { B } } { d t } = \boldsymbol { \omega } \times \boldsymbol { B }$$
となります。次に回転系で時間変化するベクトル$\bm{B}(t)$を考えます。これ以降、回転系での時間微分を表す時には$d’/dt$の記号を用いることにします。静止系での時間変化$dB/dt$は上の回転による時間変化の項に回転系での時間変化$d’\bm{B}/dt$の項が加わるので、
$$\frac { d \boldsymbol { B } } { d t } = \frac { d ^ { \prime } \boldsymbol { B } } { d t } + \boldsymbol { \omega } \times \boldsymbol { B }$$
が成り立ちます。上の式は一般のベクトルに対して成り立つので、位置ベクトルに関しても
$$\frac { d \boldsymbol { r } } { d t } = \frac { d ^ { \prime } \boldsymbol { r } } { d t } + \boldsymbol { \omega } \times \boldsymbol { r }$$
が成り立つことになります。例えば、回転系で止まっている点の運動を静止系で観察すると、その速度は
$$\boldsymbol { v } = \boldsymbol { \omega } \times \boldsymbol { r }$$
となります。$d\bm{r}/dt$を静止系でもう1回時間微分すると
$$\frac { d ^ { 2 } \boldsymbol { r } } { d t ^ { 2 } } = \frac { d } { d t } \frac { d ^ { \prime } \boldsymbol { r } } { d t } + \boldsymbol { \omega } \times \frac { d \boldsymbol { r } } { d t }$$
と書き直せます。この式は先の結果を代入することにより
$$\frac { d } { d t } \frac { d ^ { \prime } \boldsymbol { r } } { d t } = \frac { d ^ { \prime 2 } \boldsymbol { r } } { d t ^ { 2 } } + \boldsymbol { \omega } \times \frac { d ^ { \prime } \boldsymbol { r } } { d t }$$
一方、右辺第$2$項は
$$\omega \times \frac { d r } { d t } = \omega \times \left( \frac { d ^ { \prime } r } { d t } + \omega \times r \right)$$
となるため、静止系と回転系の加速度ベクトルの関係は
$$\frac { d ^ { 2 } \boldsymbol { r } } { d t ^ { 2 } } = \frac { d ^ { \prime 2 } \boldsymbol { r } } { d t ^ { 2 } } + 2 \boldsymbol { \omega } \times \frac { d ^ { \prime } \boldsymbol { r } } { d t } + \boldsymbol { \omega } \times ( \boldsymbol { \omega } \times \boldsymbol { r } )$$
となることが分かります。静止系での運動方程式が
$$m \frac { d ^ { 2 } \boldsymbol { r } } { d t ^ { 2 } } = \boldsymbol { F }$$
で表されるときは、回転系での運動方程式は
$$m \frac { d ^ { \prime 2 } \boldsymbol { r } } { d t ^ { 2 } } = \boldsymbol { F } – m \bm{\omega} \times ( \boldsymbol { \omega } \times \boldsymbol { r } ) – 2 m \boldsymbol { \omega } \times \frac { d ^ { \prime } \boldsymbol { r } } { d t }$$
となります。この式の右辺第2項が遠心力、第3項がコリオリ力を表すことが確認できます。

第15講のまとめ

最後に一言コメントをして第15講を終わりにしましょう。これまでの講義では質点の力学について扱ってきました。そして第14・15講で回転について論じました。しかし、これはある点のまわりでの質点の回転運動であって、質点の自転ではありません。質点は大きさを持たない点であるため、自転を論じることは出来ないのです。実は剛体と呼ばれる物体を新たに考えることで物体の自転も扱うことが出来るようになります。そして剛体の運動の議論は質点が複数集まった質点系の力学が基礎になります。古典力学1では、質点の運動の議論だけに留めることにして、これらについては、機会があれば古典力学2で扱うことにします。