$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}
\def\Ket#1{{\left|{#1}\right\rangle}}$

$6$頂点模型の相図

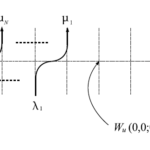
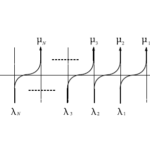
先の固有値問題に関する予想を認めたとしよう。$6$頂点模型の転送行列の固有値を$t_j~(t_1>t_2>\cdots),j=1,\cdots,2^M$とおくと、分配関数は、

\begin{equation}
Z=\mathrm{Tr}\mathcal{T}^N(u)=\sum_{j=1}^{2^M}t_j^M
\end{equation}

となる。また、$1$サイトあたりの自由エネルギー$f$は、

\begin{equation}
f=-\dfrac{kT}{NM}\ln{Z}=-\dfrac{kT}{NM}\left[\ln{t_1^N}+\ln{\left\{1+\left(\dfrac{t_2}{t_1}\right)^N+\cdots\right\}}\right]\underset{N,M\rightarrow\infty}{\longrightarrow}\lim_{N\rightarrow\infty}-\dfrac{kt}{M}\ln{t_1}
\end{equation}

と計算出来る。従って、熱力学極限においては、$\mathcal{T}(u)$の最大固有値$t_1$さえ分かれば自由エネルギーを求めることが出来る。

Bethe 仮説方程式は一般の$M$、$m$について解くことは出来ないが、$M\rightarrow\infty$の場合については厳密な解析がなされている。以下、これについて考えることにしよう。

自由エネルギー$f$は

\begin{equation}
\Delta=\dfrac{a^2+b^2-c^2}{2ab}\overset{(6)}{=}\cos{\eta}\tag{F.E.}
\end{equation}

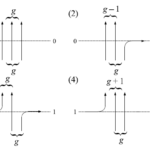
の値に応じて$4$つの場合に分けられている。これは下図のようにあらわすことが出来る。

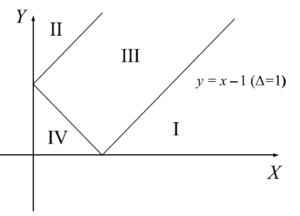
図26　$6$頂点模型の略記図

この場合分けについてそれぞれ考えてみよう。

(1)I・IIのとき
まず、I・II の場合を考えよう。これは$\Delta>1$の場合であり、強誘電相に対応している。I の場合は状態$a$が支配的となり、下図のようになる。

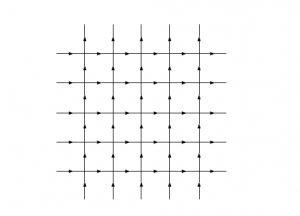
図27　$a$が支配的な場合の図

このとき、自由エネルギーは$f=-kT\ln{a(u)}$となる。一方で、II の場合は状態$b$が支配的となり、下図のようになる。

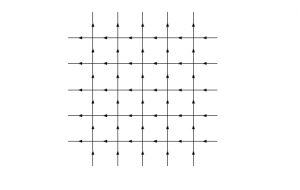
図28　$b$が支配的な場合の図

このとき、自由エネルギーは$f=-kT\ln{b(u)}$となる。

(2)IIIのとき
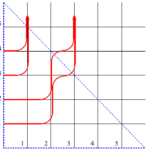
次に、III の場合を考えよう。これは$-1<\Delta<1$の場合であり、無秩序相に対応している。この場合は端のところにだけ周期的境界条件が効いており、それ以外のところは状態$a$、$b$、$c$が無秩序に現れている。これは下図の灰色の部分にあたる。

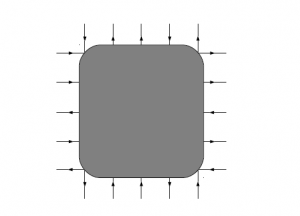
図29　$6$頂点模型の略記図

(3)IVのとき
最後に、IV の場合を考えよう。これは$\Delta<-1$の場合であり、反強誘電相に対応している。(この場合は端のところにだけ周期的境界条件が効いており、それ以外のところは状態$a$、$b$、$c$が無秩序に現れている。(F.E.)より、$\Delta$が負になるために状態$c$が支配的になっている。これは下図のようになる。

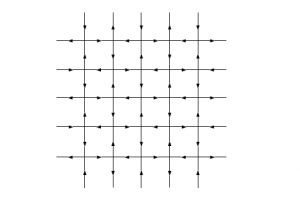
 図30　$6$頂点模型の略記図

このとき、相関長が有限になるという性質が知られている。 ここで相転移についていくつか事実を列挙しておくことにする。状態$a$、$b$、$c$のエネルギーをそれぞれ$\varepsilon_a$、$\varepsilon_b$、$\varepsilon_c$とあらわすことにすると、Boltzmann 重みは \begin{equation} a=\mathrm{e}^{-\frac{\varepsilon_a}{kT}}　、　b=\mathrm{e}^{-\frac{\varepsilon_b}{kT}}　、　c=\mathrm{e}^{-\frac{\varepsilon_c}{kT}} \end{equation} と書ける。つまり、高温極限$T\rightarrow\infty$で$a,b,c\rightarrow1$となるから、下図のように$\mathrm{I}\rightarrow\mathrm{III}$、$\mathrm{II}\rightarrow\mathrm{III}$、$\mathrm{IV}\rightarrow\mathrm{III}$という相転移が考えられる。

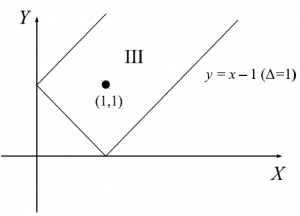
図31　$6$頂点模型の略記図

このうち、$\mathrm{I}\rightarrow\mathrm{III}$と$\mathrm{II}\rightarrow\mathrm{III}$は自由エネルギーの$T$についての$1$階微分が不連続であり、$1$次相転移であるということは知られている。一方で、$\mathrm{IV}\rightarrow\mathrm{III}$は$T$についての微分を何回しても導関数は連続であり、$\infty$次相転移であるということが知られている。$\infty$次相転移の場合の自由エネルギーは特異的であり、転移温度$T_c$と定数$A>0$を用いて、

\begin{equation}
f_c\sim\exp{\left(-\dfrac{A}{|T-T_c|^{\frac{1}{2}}}\right)}
\end{equation}

と書ける。