$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}
\def\Ket#1{{\left|{#1}\right\rangle}}$

$1$次元量子スピン鎖

今回はrational な場合を考える。さて、$6$頂点模型の転送行列$\mathcal{T}(u)$を用いて、$H^{(i)}\in\mathrm{End}(V_1\otimes\cdots\otimes V_M)$を

\begin{equation}
\dfrac{1}{i}\ln{\dfrac{\mathcal{T}(u)}{\eta^M}}=H^{(0)}+H^{(1)}u+H^{(2)}u^2+\cdots
\end{equation}

で定義する。$\mathcal{T}(u)$の可換性$[\mathcal{T}(u),\mathcal{T}(v)]=0$より、任意の$i,j=0,1,2,\cdots$で$[H^{(i)},H^{(j)}]=0$が成り立つ事が言える。ここでは、$H^{(0)}$、$H^{(1)}$を具体的に求めてみよう。

まず、$H^{(0)}$を求めてみよう。今、

\begin{equation}
H^{(0)}=\dfrac{1}{i}\ln{\dfrac{\mathcal{T}(0)}{\eta^M}}
\end{equation}

であるが、$\mathcal{T}(0)=\mathrm{Tr}_0T(0)$、$T(0)=L_M(0)\times\cdots\times L_1(0)$、$L_j(0)=R_{0j}(0)$という条件があるから、$L_j(0)=\eta P_{0j}$という式が成り立つ。下図に$P_{0j}$と$T(u)$の図をあらわした。

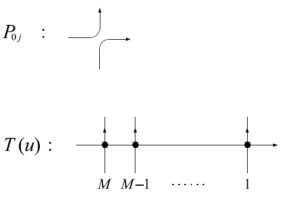
図32　$6$頂点模型の略記図

これらにより、$T(0)$と$\mathcal{T}(0)/\eta^M$は下図のようになる。

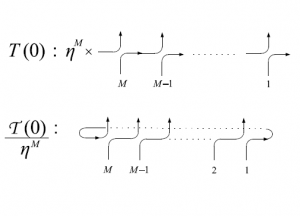
図33　$6$頂点模型の略記図

これにより、$\mathcal{T}(0)/\eta^M$はシフト演算子であると言われる。これは、

\begin{equation}
\dfrac{\mathcal{T}(0)}{\eta^M}(v_1\otimes v_2\otimes v_3\otimes\cdots\otimes v_M)=v_2\otimes v_3\otimes\cdots\otimes v_M\otimes v_1
\end{equation}

という演算子である。

問題18

$v_j\in V_i\simeq\mathbb{C}^2$の時、$\mathcal{T}(0)/\eta^M$の固有ベクトルは

\begin{equation}
\sum_{j=1}^M\exp{\left(-\frac{2n\pi i}{M}j\right)}v_j\otimes v_{j+1}\otimes\cdots\otimes v_M\otimes v_1\otimes\cdots\otimes v_{j-1}
\end{equation}

であり、固有値は$\exp{(2n\pi i/M)}$となることを示せ。但し、$n=0,1,\cdots,M-1$である。

解答18

$\exp{(2in\pi)}=\exp{(-2in\pi)}=1$であることを利用する。例えば、$M=2$のとき、

\begin{align}
&\dfrac{\mathcal{T}(0)}{\eta^2}(\exp{(-in\pi)}v_1\otimes v_2+\exp{(-2in\pi)}v_2\otimes v_1)\nonumber\\
=&\exp{(in\pi)}(\exp{(-in\pi)}v_1\otimes v_2+\exp{(-2in\pi)}v_2\otimes v_1)
\end{align}

となる。一般には、

\begin{align}
&\dfrac{\mathcal{T}(0)}{\eta^M}\sum_{j=1}^M\exp{\left(-\frac{2n\pi i}{M}j\right)}v_j\otimes v_{j+1}\otimes\cdots\otimes v_M\otimes v_1\otimes\cdots\otimes v_{j-1}\nonumber\\
=&\dfrac{\mathcal{T}(0)}{\eta^M}\biggl\{\exp{\left(-\dfrac{2in\pi\times1}{M}\right)v_1\otimes v_2\otimes\cdots\otimes v_M}\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times2}{M}\right)v_2\otimes v_3\otimes\cdots\otimes v_M\otimes v_1}+\cdots\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times (M-1)}{M}\right)v_{M-1}\otimes v_M\otimes\cdots\otimes v_{M-2}}\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times M}{M}\right)v_M\otimes v_1\otimes\cdots\otimes v_{M-1}}\biggr\}\nonumber\\
=&\biggl\{\exp{\left(-\dfrac{2in\pi\times1}{M}\right)v_2\otimes v_3\otimes\cdots\otimes v_M\otimes v_1}\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times2}{M}\right)v_3\otimes v_4\otimes\cdots\otimes v_M\otimes v_1\otimes v_2}+\cdots\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times (M-1)}{M}\right)v_M\otimes v_1\cdots\otimes v_{M-1}}\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times M}{M}\right)v_1\otimes v_2\otimes\cdots\otimes v_M}\biggr\}\nonumber\\
=&\exp{\left(\dfrac{2in\pi}{M}\right)}\biggl\{\exp{\left(-\dfrac{2in\pi\times1}{M}\right)v_1\otimes v_2\otimes\cdots\otimes v_M}\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times2}{M}\right)v_2\otimes v_3\otimes\cdots\otimes v_M\otimes v_1}+\cdots\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times (M-1)}{M}\right)v_{M-1}\otimes v_M\otimes\cdots\otimes v_{M-2}}\nonumber\\
&+\exp{\left(-\dfrac{2in\pi\times M}{M}\right)v_M\otimes v_1\otimes\cdots\otimes v_{M-1}}\biggr\}\nonumber\\
\end{align}

となる。よって題意は示された。

従って、上記のベクトルは

\begin{equation}
H^{(0)}=\dfrac{1}{i}\ln{\dfrac{\mathcal{T}(0)}{\eta^M}}
\end{equation}

の固有ベクトルであり、固有値は

\begin{equation}
\dfrac{1}{i}\ln{\exp{(\dfrac{2n\pi i}{M})}}=\dfrac{2n\pi}{M}
\end{equation}

である。これは運動量演算子のようなものである。

次に$H^{(1)}$を求めてみよう。今、

\begin{equation}
H^{(1)}=\dfrac{1}{i}\dfrac{d}{du}\left(\ln{\dfrac{\mathcal{T}(u)}{\eta^M}}\right)\biggr|_{u=0}=\dfrac{\mathcal{T}^{-1}(1)}{i}\dfrac{d\mathcal{T}(0)}{du}
\end{equation}

であるが、$dL_j(0)/du=\mathbbm{1}$なので

\begin{equation}
\dfrac{d\mathcal{T}(0)}{du}=\eta^{M-1}\sum_{j=1}^M\mathrm{Tr}_0P_{0M}\cdots P_{0j+1}\times\mathbbm{1}\times P_{0j-1}\cdots P_{01}
\end{equation}

従って、$\displaystyle\sum_{j=1}^M\mathrm{Tr}_0P_{0M}\cdots P_{0j+1}\times\mathbbm{1}\times P_{0j-1}\cdots P_{01}$の部分は下図のようになる。

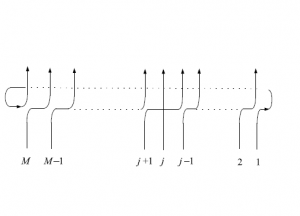
図34　$6$頂点模型の略記図

次に$\mathcal{T}^{-1}(0)\dfrac{d\mathcal{T}(0)}{du}$は下図を利用する。赤線を境にして$\mathcal{T}^{-1}(0)$と$\dfrac{d\mathcal{T}(0)}{du}$に対応している。

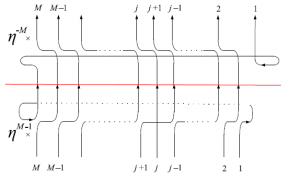
図35　$6$頂点模型の略記図

この図により、

\begin{equation}
\mathcal{T}^{-1}(0)\dfrac{d\mathcal{T}(0)}{du}=\eta^{-1}\sum_{j=1}^MP_{jj+1}
\end{equation}

結局、$H^{(1)}$は

\begin{equation}
H^{(1)}=\dfrac{1}{i\eta}\sum_{j=1}^MP_{jj+1}
\end{equation}

となる。但し、$M+1=1$と約束する。ここで、

\begin{equation}
P=\dfrac{1}{2}(\sigma^0\otimes\sigma^0+\sigma^1\otimes\sigma^1+\sigma^2\otimes\sigma^2+\sigma^3\otimes\sigma^3)
\end{equation}

であらわされるということを思い出すと、

\begin{equation}
H^{(1)}=\dfrac{1}{2i\eta J}H_{XXX}+\dfrac{M}{2i\eta}\mathbbm{1}
\end{equation}

となる。但し、$J\in\mathbb{R}$であり、$H_{XXX}$は

\begin{equation}
H_{XXX}=J\sum_{j=1}^M(\sigma^0\otimes\sigma^0+\sigma^1\otimes\sigma^1+\sigma^2\otimes\sigma^2+\sigma^3\otimes\sigma^3)
\end{equation}

となる。これはまさに$1$次元Heisenberg 模型であり、$XXX$模型などとも呼ばれる。

問題19

Trigonometric matrix の場合(6)では、$H^{(i)}\in\mathrm{End}(V_1\otimes\cdots\otimes v_M)$を

\begin{equation}
\dfrac{1}{i}\ln{\dfrac{\mathcal{T}(u)}{(\sin{\eta})^M}}=H^{(0)}+H^{(1)}u+H^{(2)}u^2+\cdots
\end{equation}

と定義すると、

\begin{equation}
H^{(1)}=\dfrac{1}{2i\sin{(\eta)}J}H_{XXZ}+\dfrac{M\Delta}{2i\sin{(\eta)}}\mathbbm{1}
\end{equation}

となることを示せ。但し、$J\in\mathbb{R}$、$\Delta=\cos{(\eta)}$である。また、

\begin{equation}
H_{XXZ}=J\sum_{j=1}^M(\sigma^1_j\sigma^1_{j+1}+\sigma^2_j\sigma^2_{j+1}+\Delta\sigma^3_j\sigma^3_{j+1})
\end{equation}

である。この模型は$XXZ$模型と呼ばれている。

解答19

今、Trigonometric matrix の場合を考えているから、行列$R$の定義は

\begin{equation}
R=\dfrac{\sin{(u+\eta)}+\sin{u}}{2}\sigma^0\otimes\sigma^0+\dfrac{\sin{\eta}}{2}\sigma^1\otimes\sigma^1+\dfrac{\sin{\eta}}{2}\sigma^2\otimes\sigma^2+\dfrac{\sin{(u+\eta)}-\sin{u}}{2}\sigma^3\otimes\sigma^3
\end{equation}

と変更される。これにより$L_j(0)$、及び$P_{0j}$が

\begin{equation}
L_j(0)=\sin{\eta}P_{01}　、　P_{0j}=\dfrac{dR_{0j}(u)}{du}\biggr|_{u=0}=\dfrac{\cos{\eta}+1}{2}\sigma^0\otimes\sigma^0+\dfrac{\cos{\eta}-1}{2}\sigma^3\otimes\sigma^3
\end{equation}

と変わることになる。これを考慮すれば直ちに所望の結果を得る。勿論、上の式は、$\eta\rightarrow0$の極限で$L_j(0)=\eta P_{0j}$、$P_{0j}=\mathbbm{1}$に一致する。