$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}
\def\Ket#1{{\left|{#1}\right\rangle}}$
Yang-Baxter 方程式1
これ以降では、代数的Bethe 仮説法をランダムウォークなどに応用することを考えてみる。これらの議論についてはBorodin-Petrov のレクチャーノート、及び論文を参照すると良い。実は、一度広義的に模型を定義して、その後にある種の解析接続を行なうことで、Borodin-Petrov の理論が得られると考えられている。
模型の定義
集合$P$を$\mathbb{Z}_{\geq1}$におけるup-right path の集合と定義する。但し、条件として、次の$3$つを課す。
- 全てのpath は左側の境界$\{(1,m):m\in\mathbb{Z}_{\geq1}\}$から入る。
- 水平な辺は$2$つ以上のpath によって共有されない。
- 垂直な辺は複数のpath によって共有されても良い。
今、$\mathbb{Z}^2$なので、正方格子を考える。例えば、下図のような格子を考えてみよう。
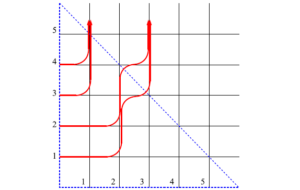
図36 $6$頂点模型の略記図
今、$P$の上の確率測度を以下のように定める。
\begin{equation}
\left\{
\begin{array}{rcl}
T_n&\coloneqq&\{(x,y)\in\mathbb{Z}^2_{\geq1}:x+y=n\}\\
&&\\
P_n&\coloneqq&P\cap T_n
\end{array}
\right.
\end{equation}
$P$の上の確率測度が定まっているという仮定の下で$P_{n+1}$を次のように定める。
- $x+y=n$で定まる$P_n$の境界点$(x,y)$に下の辺から$(x,y)$に向かうpath の数$i_1\in\mathbb{Z}_{\geq1}$と左の辺から$(x,y)$に向かうpath の数$j_1\in\{0,1\}$は確定している。
- 全ての$(x,y)$に対して独立に$(x,y)$から上へ向かうpath の数$i_2$と右へ向かうpath の数$j_2$を次のウェイトに従って決める。
\begin{equation}
\left\{
\begin{array}{rcl}
P((i_1,0)\rightarrow(i_2,0))&=&\dfrac{1+q^{i_1}su_y}{1-su_y}\mathbbm{1}_{i_1=i_2}\\
&&\\
P((i_1,0)\rightarrow(i_2,1))&=&\dfrac{(q^{i_1}-1)su_y}{1-su_y}\mathbbm{1}_{i_1=i_2+1}\\
&&\\
P((i,1)\rightarrow(i_2,1))&=&\dfrac{s^2q^{i_1}-su_y}{1-su_y}\mathbbm{1}_{i_1=i_2}\\
&&\\
P((i_1,1)\rightarrow(i_2,0))&=&\dfrac{1-s^2q^{i_1}}{1-su_y}\mathbbm{1}_{i_1=i_2-1}
\end{array}
\right.
\end{equation}
但し、$\mathbbm{1}_{(式)}$は$(式)$を満たすなら$1$、満たさないなら$0$を返すというものである。これらによって、$P$について、以下の$2$つの性質が分かる。
図37 $6$頂点模型の略記図
\begin{equation}
\left\{
\begin{array}{rcl}
\displaystyle\sum_{i_2,j_2}P((i_1,j_1)\rightarrow(i_2,j_2))&=&1\\
&&\\
P((i_1,j_1)\rightarrow(i_2,j_2)&=&0~\mathrm{if}~i_1+j_1\neq i_2+j_2
\end{array}
\right.
\end{equation}
従って、上の$4$つのウェイトが非負ならば、このような操作は$P_{n+1}$の上の確率測度を定め、さらに$P$の上の確率測度に一意的に拡張されることが言える。
さて、前述の主張と必要十分条件ではないが、よく用いるウェイトが非負であるような$q$、$u_y$、$s$には以下のようなものがある。
\begin{equation}
\left\{
\begin{array}{rcl}
1&:&q\in(0,1)、u_y>0、s\in(-1,0)\\
&&\\
2&:&u_1=u_2=\cdots=u>q^{-I}、s=q^{-\frac{I}{2}}、I=1,2,\cdots
\end{array}
\right.
\end{equation}
では何故、このような複雑なモデルを考える必要があるのだろうか。それは$1$と$2$がそれぞれ重要な模型と対応しているからである。これを以下で順番に見ることにしよう。
$1$の場合
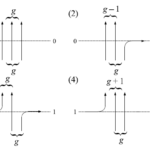
特に、$u_1=u_2=\cdots=-a/s~(a>0)$として$s\rightarrow0_-$の極限を考える。
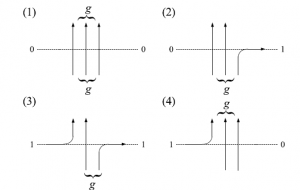
図38 $6$頂点模型の略記図
このときのウェイトは左から順に$1-(1-q^g)\beta$、$(1-q^g)\beta$、$\beta$、$1-\beta$と書くことが出来る。但し、$\beta=a/(a+1)$であり、$0<\beta<1$となる。
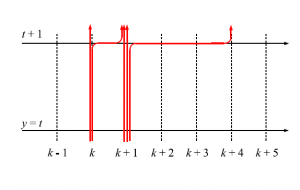
図39 $6$頂点模型の略記図
これを確率的$6$頂点模型、または高次元スピン頂点模型(heigher spin vertex model)と呼ぶ。
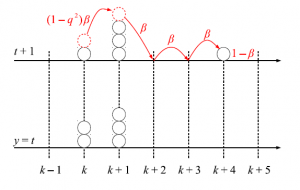
図40 $6$頂点模型の略記図
これはゼロレンジプロセスと言う。ゼロレンジプロセスにおけるサイト$k$の粒子数と排他過程における$k-1$番目と$k$番目の粒子間に空いたサイトの数には対応関係がある。以上の高次元スピン頂点模型は以下のルールの下で排他過程に対応している。
- 各時間ステップで、小さい番号の粒子から順に動かしていく。このようなルールをsequential update という。
- $k$番目の粒子は、$k-1$番目の粒子が動いた場合、確率$\beta$で右に$1$マス動き、確率$1-\beta$でその場に留まる。逆に$k-1$番目の粒子が動かなかった場合、確率$(1-q^{\mathrm{gap}})\beta$で右に$1$マス動き、確率$1-(1-q^{\mathrm{gap}})\beta$でその場に留まる。但し、$\mathrm{gap}$は$k-1$番目と$k$番目の間の空サイトの個数をあらわしている。
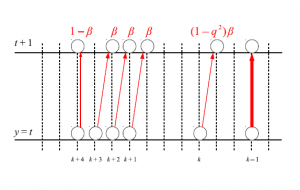
図41 $6$頂点模型の略記図
このような排他過程をBernoulli $q$-TASEP という。これはMacdonald 多項式と相性が良い確率過程であることが知られている。
$2$の場合
$I=1$の場合のウェイトは
図42 $6$頂点模型の略記図
となる。但し、$\delta_1$と$\delta_2$はそれぞれ、
\begin{equation}
\delta_1=\dfrac{1-q^{\frac{1}{2}}u}{1-q^{-\frac{1}{2}}u} 、 \delta_2=\dfrac{q^{-1}-q^{-\frac{1}{2}}u}{1-q^{\frac{1}{2}}u}
\end{equation}
となる。今、簡単な計算により、
\begin{equation}
P((I,1)\rightarrow(I+1,0))=\dfrac{1-q^{-I}q^I}{1-q^{-\frac{I}{2}}}u_y=0
\end{equation}
が明らかに成り立っているということに注意せよ。この模型は確率的$6$頂点模型という。
まとめ
高次元スピン頂点模型は$1$の場合は$q$-TASEP になる。一方で、$2$の場合は確率的$6$頂点模型(ASEP)になっている。この意味で、高次元スピン頂点模型は統一的な模型であると言える。因みに、$1$に場合も$2$の場合も$q\rightarrow0$とすればTASEP となる。
前回の復習として、確率的$6$頂点模型の例をもう$1$つ挙げておく。
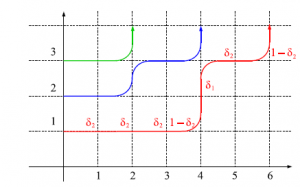
図43 $6$頂点模型の略記図
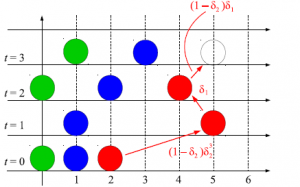
図44 $6$頂点模型の略記図
ここからの目標
ここからの目標を述べる。ここからはhsvm において、以下の量を定める。
$h:\mathbb{Z}_{\geq1}\longrightarrow\mathbb{Z}_{\geq0}$
$h(x,t):$頂点$(x,t)$上またはその右側を横切る経路の本数
注意として、$q$-TASEP とs6v では、
1. $q$-TASEP:$h(x,t)\mapsto$$x-1$番目の粒子の時刻$t$にいる位置
2. s6v$h(x,t)\mapsto$粒子の流れ
つまり、まず$\bm{E}=[\prod_{i=1}^lq^{h(x_i,t)}]$の積分表示を求める。これにより、$x_1=x_2=\cdots=x$とすると、$h(x,t)$の$l$次モーメント$\bm{E}=[q^{lh(x,t)}]$を知ることが出来て、これによって$h(x,t)$の分布を得ることが出来る。