$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}
\def\Ket#1{{\left|{#1}\right\rangle}}$
高次元スピン頂点模型の分配関数と対称関数2
ここでは演算子$D_L$の$L\rightarrow\infty$の極限を考えたい。わざわざ回を分けたのは、$A$、$B$のように素朴に$L\rightarrow\infty$の極限を取ると上手くいかないからである。
演算子$\bar{D}$と対称関数$G^c_{\lambda/\mu}(u_1,\cdots,u_n)$
素朴に拡張すると下図のようになる。
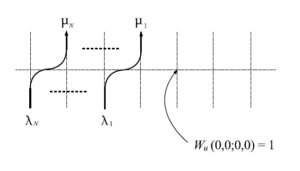
図57 高次元スピン頂点模型の略記図
$\lambda_1<L$となるような$L$を固定し、それ以降の頂点に
\begin{equation}
W_u(0,1;0,1)=\dfrac{u-s}{1-su}
\end{equation}
を割り当てる。このようにすると、常に$(\frac{u-s}{1-su})^\infty$という無限積を含むことになってしまうため、都合が悪い。そこで、各頂点について$W_u(0,1;0,1)$で割るという、ある種の正規化を行う。このときのウェイトの変換則は次の通り。
\begin{equation}
\dfrac{W_u(g,0;g,0)}{W_u(0,1;0,1)}=\dfrac{1-sq^gu}{u-s}=W_{u^{-1}}(g,1;g,1)=W^c_{u^{-1}}(g,1;g,1)
\end{equation}
同様に、
\begin{equation}
\dfrac{W_u(g+1,0;g,1)}{W_u(0,1;0,1)}=W^c_{u^{-1}}(g,1;g+1,0)
\end{equation}
\begin{equation}
\dfrac{W_u(g,1;g+1,0)}{W_u(0,1;0,1)}=W^c_{u^{-1}}(g+1,0;g,1)
\end{equation}
\begin{equation}
\dfrac{W_u(g,1;g,1)}{W_u(0,1;0,1)}=W^c_{u^{-1}}(g,0;g,0)
\end{equation}
が成り立つ。まとめると、
\begin{equation}
\dfrac{W_u(i_1,j_1;i_2,j_2)}{W_u(0,1;0,1)}=W^c_{u^{-1}}(i_2,1-j_1;i_1,1-j_2)
\end{equation}
となる。
問題23
上の式を確かめよ。
解答23
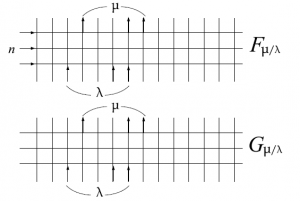
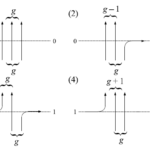
図45 高次元スピン頂点模型の略記図
| $W_u(i_1,j_1;i_2,j_2)$ | $(1)$ | $(2)$ | $(3)$ | $(4)$ |
| $W_u(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{(1-s^2q^{g-1})u}{1-su}$ | $\dfrac{u-sq^g}{1-su}$ | $\dfrac{1-q^{g+1}}{1-su}$ |
| $W_u^c(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{(1-q^g)u}{1-su}$ | $\dfrac{u-sq^g}{1-su}$ | $\dfrac{1-s^2q^g}{1-su}$ |
| $L_u(i_1,j_1;i_2,j_2)$ | $\dfrac{1-sq^gu}{1-su}$ | $\dfrac{-su(1-q^g)}{1-su}$ | $\dfrac{-s(u-sq^g)}{1-su}$ | $\dfrac{1-s^2q^g}{1-su}$ |
表2 Yang-Baxter 方程式
上の図と表を用いると、例えば、
\[
\dfrac{W_u(g,0;g,0)}{W_u(0,1;0,1)}\dfrac{\dfrac{1-sq^gu}{1-su}}{\dfrac{u-s}{1-su}}=\dfrac{1/u-sq^g}{1-s/u}=W_{u^{-1}}(g,1;g,1)=W^c_{u^{-1}}(g,1;g,1)
\]
と示せる。他の$3$式も同様にして確認出来る。よって題意は示された。
従って、
\begin{equation}
\mathrm{Weight}(図58)\times\dfrac{1}{(W_u(0,1;0,1))^{L+1}}=\mathrm{Weight}(図59)\times\dfrac{c(\lambda)}{c(\mu)}
\end{equation}
となる。ここで大事なのは$u\rightarrow u^{-1}$となっていることと$\lambda\leftrightarrow\mu$とひっくり返っていることである。
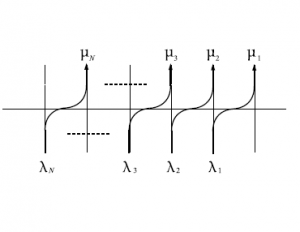
図58 $6$頂点模型の略記図
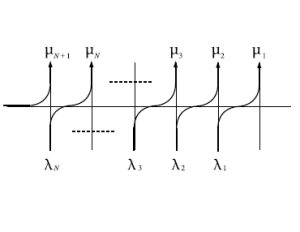
図59 $6$頂点模型の略記図
但し、
\begin{equation}
c(\nu)=\prod_k\dfrac{(s^2;q)_{n_k}}{(q;q)_k} , \nu=0^{n_0}1^{n_1}2^{n_2}\cdots , (x;q)_n=(1-x)(1-xq)\cdots(1-xq^{-1})
\end{equation}
である。$\mathrm{Weight}(図59)$のところで$L\rightarrow\infty$とすると$G_{\lambda/\mu}(u^{-1})$となる。従って、正規化された演算子$\bar{D}(u)$を
\begin{equation}
\bar{D}(u)e_\lambda=\sum_{\mu\in\mathrm{Sign}^+_N}\underbrace{\dfrac{c(\lambda}{c(\mu)}G_{\lambda/\mu}(u^{-1})}_{\coloneqq G^c_{\lambda/\mu}(u^{-1})}e_\mu
\end{equation}
で定義する。更に$G^c_{\lambda/\mu}(u_1,\cdots,u_n)$を
\begin{equation}
\bar{D}(u_1)\bar{D}(u_2)\cdots\bar{D}(u_n)e_\lambda=\sum_{\mu\in\mathrm{Sign}^+_N}G^c_{\lambda/\mu}(u_1,\cdots,u_n)e_\mu
\end{equation}
と定義する。$G_{\lambda/\mu}(u^{-1})$は対称関数だったので、$G^c_{\lambda/\mu}(u)$も明らかに対称関数である。
Yang-Baxter 方程式とCauchy 型恒等式
Yang-Baxter 方程式(4)の$4$番目の式、
\begin{equation}
B_L(u_1)D_L(u_2)=\dfrac{u_1-u_2}{qu_1-u_2}D_L(u_2)B_L(u_1)+\dfrac{(1-q)u_2}{u_2-qu_1}B_L(u_2)D_L(u_1)
\end{equation}
の$L\rightarrow\infty$の極限を考える。両辺を$(W_{u_2}(0,1;0,1))^{L+1}$で割ると、
\begin{align}
&B_L(u_1)\dfrac{D_L(u_2)}{(W_{u_2}(0,1;0,1))^{L+1}}\nonumber\\
=&\dfrac{u_1-u_2}{qu_1-u_2}\dfrac{D_L(u_2)}{(W_{u_2}(0,1;0,1))^{L+1}}B_L(u_1)+\dfrac{(1-q)u_2}{u_2-qu_1}B_L(u_2)\dfrac{D_L(u_1)}{(W_{u_1}(0,1;0,1))^{L+1}}\left(\dfrac{W_{u_1}(0,1;0,1)}{W_{u_2}(0,1;0,1)}\right)^{L+1}\nonumber
\end{align}
となる。今後は$(\frac{W_{u_1}(0,1;0,1)}{W_{u_2}(0,1;0,1)})^{L+1}$が有限の領域、つまり、
\begin{equation}
\left|\frac{W_{u_1}(0,1;0,1)}{W_{u_2}(0,1;0,1)}\right|^{L+1}=\left|\dfrac{u_1-s}{1-su_1}\dfrac{1-su_2}{u_2-s}\right|<1
\end{equation}
を満たす場合を考える。さて、このとき、
\begin{equation}
B(u_1)\bar{D}(u_2)=\dfrac{u_1-u_2}{qu_1-u_2}\bar{D}(u_2)B(u_1)\tag{2}
\end{equation}
となる。$F_{\mu/\nu}(u)$、$G^c_{\lambda/\mu}(v)$を用いると(2)は次のように書き換えることが出来る。$u,v\in\mathbb{C}$が条件
\begin{equation}
\left|\dfrac{u-s}{1-su}\dfrac{v-s}{1-sv}\right|<1\tag{3}
\end{equation}
を満たすとき、
\begin{equation}
\sum_{\kappa\in\mathrm{Sign}}G^c_{\kappa/\lambda}(v)F_{\kappa/\nu}(u)=\dfrac{1-quv}{1-uv}\sum_{\kappa\in\mathrm{Sign}}F_{\lambda/\mu}(u)G^c_{\nu\mu}(v)\tag{4}
\end{equation}
を満たす。これをCauchy 恒等式という。以上の議論から分かったように、この恒等式はYang-Baxter 方程式からの帰結である。以後、$u,v\in\mathbb{C}$が(3)を満たすとき、$(u,v)\in\mathrm{Adm}$と書くことにする。
$u_1,\cdots,u_M,v_1,\cdots,v_N\in\mathbb{C}$は、$(u_i,v_j)\in\mathrm{Adm},i=1,\cdots,M,j=1,\cdots,N$とする。このとき、
\begin{align}
&\sum_{\kappa\in\mathrm{Sign}^+}G^c_{\kappa/\lambda}(v_1,\cdots,v_N)F_{\kappa/\nu}(u_1,\cdots,u_M)\nonumber\\
=&\prod_{i=1}^M\prod_{j=1}^N\dfrac{1-qu_iv_j}{1-u_iv_j}\sum_{\mu\in\mathrm{Sign}^+}F_{\lambda/\mu}(u_1,\cdots,u_M)\times G^c_{\nu/\mu}(v_1,\cdots,v_M)\tag{5}
\end{align}
を満たすことが分かる。
(5)で$v=\phi$、$\lambda=0^M$を代入すると、
\begin{equation}
F_{0^M}(u_1,\cdots,u_M)\coloneqq F_{0^M/\phi}(u_1,\cdots,u_M)=\dfrac{(q:q)_M}{\displaystyle\prod_{i=1}^M(1-su_i)}
\end{equation}
となる。ここで、$G^c_\phi(u_1,\cdots,u_N)\coloneqq G^c_{\phi/\phi}(u_1,\cdots,u_N)=1$に注意すると、
\begin{align}
&\sum_{\kappa\in\mathrm{Sign}^+_N}G^c_{\kappa/\lambda}(v)F_\kappa(u_1,\cdots,u_N))\nonumber\\
=&\prod_{i=1}^N\dfrac{1-qu_iv}{1-u_iv}F_\lambda(u_1,\cdots,u_N)\tag{6}
\end{align}
但し、
\begin{equation}
F_\kappa\coloneqq F_{\kappa/\phi} , \lambda\in\mathrm{Sign}^+_N , (v,u_i)\in\mathrm{Adm} , i=1,\cdots,N
\end{equation}
\begin{equation}
\sum_{k\in\mathrm{Sign}^+_{N+1}}G^c_{\kappa}(v_1,\cdots,v_n)F_{\kappa/\nu}(u)=\dfrac{1-q^{N+1}}{1-su}\prod_{j=1}^n\dfrac{1-quv_j}{1-uv_j}G^c_\nu(v_1,\cdots,v_n)\tag{7}
\end{equation}
但し、
\begin{equation}
G^c_\kappa\coloneqq G^c_{\kappa/0^N} , \nu\in\mathrm{Sign}^+_N , (v_i,u)\in\mathrm{Adm} , i=1,\cdots,n
\end{equation}
\begin{equation}
\sum_{\kappa\in\mathrm{\mu\in\mathrm{Sign}^+_M}}F_\mu(u_1,\cdots,u_M)G^c_\mu(v_1,\cdots,v_N)=\dfrac{(q;q)_M}{\displaystyle\prod_{i=1}^M(1-su_i)}\prod_{i=1}^M\prod_{j=1}^N\dfrac{1-qu_iv_i}{1-u_iv_j}\tag{8}
\end{equation}
注意として、(8)はMacdonald 多項式のCauchy 多項式と類似の式である。