$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}$

統計力学の復習

この講義では統計力学、特にカノニカル分布の計算をする場面があるため、まずこれについて簡単に復習を行う。

統計力学とは、ミクロな物理法則からマクロな物理法則を理解する学問分野である。これは例えば、Newton の運動方程式やSchrodinger 方程式などのミクロな世界における基礎方程式から、熱力学的な温度や圧力の関係、相転移の様子などのマクロな物理法則を理解するということである。

統計力学のカノニカル分布では、分配関数$Z$が分かれば様々な物理量が計算できる。例えば、Helmholtz の自由エネルギー$F$とエントロピー$S$はそれぞれ次のように計算出来る。
\begin{equation}
F=-k_BT\ln{Z}
\end{equation}
\begin{equation}
S=-\dfrac{\partial F}{\partial T}
\end{equation}
$k_B$はBoltzmann 定数であり、$T$は温度である。

$6$頂点模型の概略

6頂点模型は統計力学における重要なモデルの1つで、1935年頃にL.Pauling が2次元の氷のモデルとして初めて導入した。

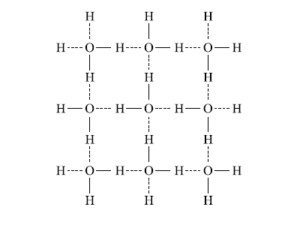
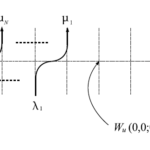
図1　6頂点模型の概略図

図において、各頂点上にO が、各辺上にH が置かれている。O は酸素原子、H は水素原子をあらわしている。また、実践の部分は共有結合をあらわしており、ここの結合によって水分子を作っている。すなわち、H は1つのO と、O は2つのH と共有結合している。そして、点線の部分は分子間力をあらわしている。

1つの頂点とその周りの4辺に注目する。各辺は実線または点線となり、4辺は2つが実線で他の2つが点線となる。よって$_4\mathrm{C}_2=6$通りの状態がある。ここで更に、後の便宜のために以下のように矢印での略記法を導入する。

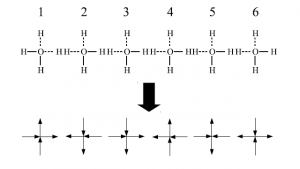
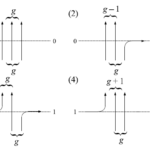
図2　6頂点模型の略記図

図のように、実線は頂点へ向かう矢印に対応し、点線は頂点から出ていく矢印に対応している。このときのそれぞれのBoltzmann 重みを左の図から順にそれぞれ$\omega_1$、$\omega_2$、$\omega_3$、$\omega_4$、$\omega_5$、$\omega_6$と割り当てる。但し、4辺の矢印を全て反対向きにしたときの対称性から、$\omega_1=\omega_2=a>0$、$\omega_3=\omega_4=b>0$、$\omega_5=\omega_6=c>0$となるはずである。今、4辺は2つが実線で他の2つが点線となるというルールがあるからこれら以外のBoltzmann 重み、例えば4辺全ての矢印が頂点へ向かうような図の重みは$0$とみなす。

頂点模型とは一般に、各頂点で局所的なエネルギーあるいはBoltzmann 重みが決まっているような模型のことを指す。ここでは6頂点模型の分配関数を求めることを考える。

まず、説明のためにいくつかの文字を定義しよう。$V$を頂点全体の集合とする。すなわち
\begin{equation}
V=\{(i,j)|i=1,2,\cdots,N~\mathrm{and}~j=1,2,\cdots,M\}
\end{equation}
と定義する。これは$N$行$M$列の図を考えるための準備である。つまり、実は図1は$N=M=3$の場合の6頂点模型の絵だったということである。

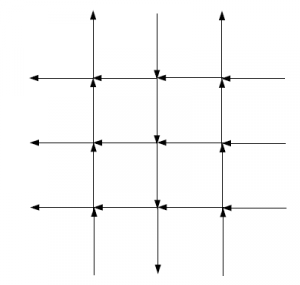
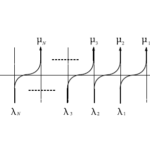
図3　$N=M=3$の6頂点模型の略記図

また、$C$を矢印の配置全体の集合、$s\in C$をそれぞれの状態と定義する。つまり、図1を1つの絵と考えたとき、$C$は全ての絵をあらわし、$s$は$C$に属する全ての絵のうちのどれか特定の1つの絵をあらわしているということである。

さて、上記のように文字を定義すると、状態$s$の出現確率は次のようになる。
\begin{equation}
\dfrac{W(s)}{Z}~\mathrm{where}~W(s)=\prod_{(i,j)\in V}w_{ij}(s)
\end{equation}
ここで$w_{ij}(s)$は状態$s$における頂点$(i,j)$のBoltzmann 重みをあらわしている。これによって、$W(s)$で状態$s$という1つの絵があらわせているのである。$Z$は分配関数で、$Z\coloneqq\sum_{s\in C}W(s)$と定義されている。統計力学の教えるところによれば、$w_{ij}(s)=\mathrm{e}^{-\beta E_{ij}(s)}$とあらわすことが出来るということが知られている。但し、$E_{ij}(s)$は状態$s$における頂点$(i,j)$の局所的なエネルギーである。また、$\beta\coloneqq(k_BT)^{-1}$であり、$k_B$はBoltzmann 定数であり、$T$は温度である。

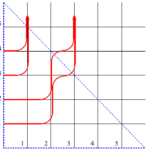
$N=1$の場合を考えよう。このとき、$i_1$と$i_1’$が同じ矢印で、かつ$j_k$と$j_k’~(k=1,\cdots,M)$が同じ矢印であるという周期的境界条件を課す。このとき、下図のようになる。

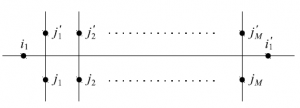
図4　$N=1$の6頂点模型

特に$N=M=1$の場合を見てみよう。今述べたように、$j_1$と$j_1’$が同じ矢印であるから周期的境界条件から$\omega_5$、$\omega_6$は取り得ない。故に分配関数は$Z=2(a+b)$となる。

問題01

以下の場合の分配関数$Z$を求めよ。
(1)周期的境界条件で、$N=1$、$M=2$
(2)周期的境界条件で、$N=1$、$M\geq1$
(3)周期的境界条件で、$N=2$、$M=2$

解答01

絵を描いてみると、以下のように直ちに求まる。
(1)$Z_{12}=4(a^2+ab+b^2)$
(2)$Z_{1M}=2^M\displaystyle\sum_{m=0}^Ma^{M-m}b^m$
(3)$Z_{22}=4(a^4+2a^2b^2+b^4)+2c^4=\{2(a^2+b^2)\}^2+2c^4$

この講義の前半はこの分配関数$Z$を解析することが目的である。これによって、物理量の熱力学極限（$N/M$を一定にして$N\rightarrow\infty$、$M\rightarrow\infty$）を考えることが出来るからである。しかし、問題01をやって分かったように、一般的にやるのはかなり大変である。これに対する$Z$の計算手法として、後で我々は代数的Bethe 仮説法という手法を学ぶ。