$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\def\mathbbm#1{{\mbox{#1}\hspace{-0.20em}\mbox{l}}}$

分配関数再考

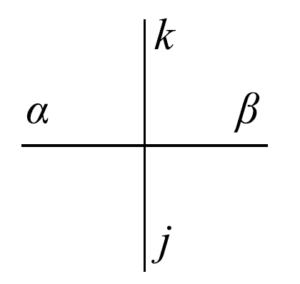
図10 $6$頂点模型における頂点

まず初めに$6$頂点模型の分配関数をあらわすことを考えよう。この模型ではBoltzmann 重みは6通り選ぶことが出来た。ここで、図10のように着目している1つの頂点に関与する4つの道それぞれの矢印の向きをあらわす変数として$\alpha,\beta,j,k\in\{1,2\}$を導入する。そして、これに対応するBoltzmann 重みを$R^{\alpha\beta,jk}$とする。$\rightarrow$、$\uparrow$、すなわち頂点から出て行く向きの矢印に対して$1$を割り当て、$\leftarrow$、$\downarrow$、すなわち頂点へ入って来る向きの矢印に対して$2$を割り当てる。

図11のように対応させると、$R^{11,11}=R^{22,22}=a$、$R^{11,22}=R^{22,11}=b$、$R^{12,21}=R^{21,12}=c$とすることが出来る。これら6つ以外、例えば、$R^{21,21}$などは全て$0$となるように考える。

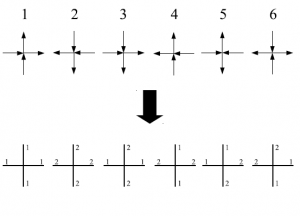
図11 $6$頂点模型の略記図

これによって、分配関数をシンプルに書き下すことが出来るようになる。下図のように、$N\times M$正方行列で考えて、周期的境界条件$\alpha_i=\alpha_i’=1~\mathrm{or}~2~(i=1,\cdots,N)$、かつ$k_j=k_j’=1~\mathrm{or}~2~(j=1,\cdots,M)$を課す。

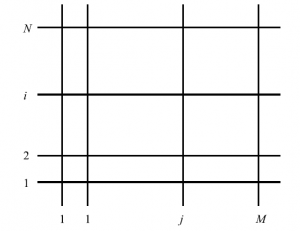
図12 $6$頂点模型の略記図

このような設定を決めると、$6$頂点模型の分配関数は以下のように書くことが出来る。
\begin{equation}
Z=\sum_{\{\alpha_{ab}\}\{j_{ab}\}}\prod_{a=1}^N\prod_{b=1}^MR^{\alpha_{ab}\alpha_{ab+1},j_{ab}j_{a+1b}}
\end{equation}
$R^{\alpha_{ab}\alpha_{ab+1},j_{ab}j_{a+1b}}
$のところは、図13より、頂点$(a,b)$の周りの矢印の情報を含んでいるということが分かる。但し、この時、周期的境界条件$\alpha_{a,1}=\alpha_{a,M+1}$、かつ$j_{1,b}=j_{N+1,b}$を加えている。

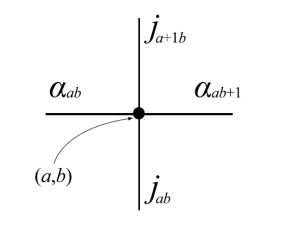
図13 $6$頂点模型の略記図

転送行列

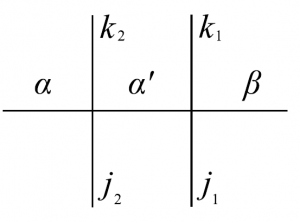
図14 $6$頂点模型の略記図

前節で求めた分配関数を転送行列を用いてあらわすことを考えてみよう。まず、$N=1$、$M=2$の自由な境界条件を考える。

この時、分配関数は$R$が2つ出てきて以下のようになる。
\begin{equation}
Z=R^{\alpha\alpha’,j_2k_2}R^{\alpha’\beta,j_1k_1}
\end{equation}
ここで、$R\in\mathrm{End}(V_0\otimes V_1)$であり、$V_0$、$V_1$は2次元複素ベクトル空間である。この時、$R$は$R^{\alpha\beta,jk}$を成分としてもつ行列とする。つまり、今、$4\times4$行列である。なお、$V_0$、$V_1$は以下のような直和で書ける。
\begin{equation}
\left\{
\begin{array}{lclcclc}
V_0&=&\mathbb{C}&\leftarrow&\oplus&\mathbb{C}&\rightarrow\\
\\
V_1&=&\mathbb{C}&\uparrow&\oplus&\mathbb{C}&\downarrow
\end{array}
\right.
\end{equation}

問題07

$R$が以下のようにあらわされることを確認せよ。
\begin{equation}
R=\left(
\begin{array}{cccc}
a&0&0&0\\
0&b&c&0\\
0&c&b&0\\
0&0&0&a
\end{array}
\right)
\end{equation}

解答07

以前の図と比較すれば、$R^{11,11}=R^{22,22}=a$、$R^{11,22}=R^{22,11}=b$、$R^{12,21}=R^{21,12}=c$とすることが出来る。これら6つ以外、例えば、$R^{21,21}$などは全て$0$となるように図を定義していたので、確かに$R$は与えられた形であらわされる。

これを用いると分配関数は
\begin{equation}
R^{\alpha\alpha’,j_2k_2}R^{\alpha’\beta,j_1k_1}=(R_{02}R_{01})^{\alpha\beta,j_1k_1,j_2k_2}
\end{equation}
とあらわされる。但し、$R_{02},R_{01}\in\mathrm{End}(V_0\otimes V_1\otimes V_2)$であり、これは$8\times8$行列になる。また、
\begin{equation}
\left\{
\begin{array}{rclcclc}
V_0&=&\mathbb{C}&\leftarrow&\oplus&\mathbb{C}&\rightarrow\\
\\
V_1~\mathrm{or}~V_2&=&\mathbb{C}&\uparrow&\oplus&\mathbb{C}&\downarrow
\end{array}
\right.
\end{equation}
$R_{02}$は$V_0$と$V_2$について$R$で作用し、$V_1$については自明に作用する。これに対して、$R_{01}$は$V_0$と$V_1$について$R$で作用し、$V_2$については自明に作用する。すなわち、
\begin{equation}
\left\{
\begin{array}{l}
(R_{02})^{\alpha\alpha’,j_1j_1′,j_2j_2′}=R^{\alpha\alpha’,j_2j_2′}\delta^{j_1j_1′}\\
\\
(R_{01})^{\alpha\alpha’,j_1j_1′,j_2j_2′}=R^{\alpha\alpha’,j_1j_1′}\delta^{j_2j_2′}
\end{array}
\right.
\end{equation}
である。このことを思い出せば、以下のことが容易に分かる。
\begin{equation}
(R_{02}R_{01})^{\alpha\beta,j_1k_1,j_2k_2}=R^{\alpha\alpha’,j_2j_2′}\delta^{j_1j_1′}R^{\alpha\alpha’,j_1j_1′}\delta^{j_2j_2′}R^{\alpha\alpha’,j_2k_2}=R^{\alpha\alpha’,j_2k_2}R^{\alpha’\beta,j_1k_1}
\end{equation}
これらをイメージ図で書いたものが図15である。

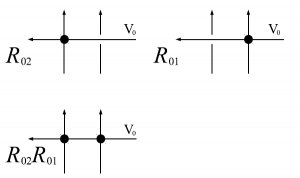
図15 $6$頂点模型の略記図

図16のように$N=1$、$M=2$で水平方向だけ周期的境界条件が課されている場合（$\alpha=\alpha’$）を考えよう。この時、分配関数は
\begin{equation}
(R_{02}R_{01})^{\alpha\alpha,j_1k_1,j_2k_2}=(\mathrm{tr}_0R_{02}R_{01})^{j_1k_1,j_2k_2}
\end{equation}
と書くことが出来る。この時の$\mathrm{tr}_0R_{02}R_{01}\in\mathrm{End}(V_1\otimes V_2)$こそが転送行列に他ならない。

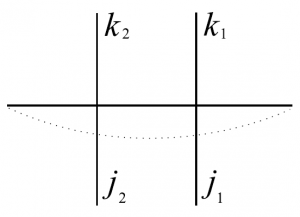
図16 $6$頂点模型の略記図

図17のように$N=M=2$で水平方向だけ周期的境界条件が課されている場合（$\alpha=\alpha’$）を考えよう。この時、分配関数は
\begin{equation}
Z=\mathrm{tr}(\mathrm{tr}_0R_{02}R_{01})^2
\end{equation}
と書くことが出来る。赤い点線のところが行列の積（和を取る作業）に対応していて、青い点線のところがトレースに対応している。

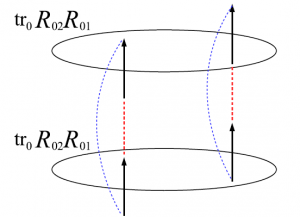
図17 $6$頂点模型の略記図

問題08

$N=M=2$とする。

(1)水平方向は周期的境界条件で、垂直方向は自由な境界条件であるとき、分配関数が
\begin{equation}
Z=\bigl\{(\mathrm{tr}_0R_{02}R_{01})^2\bigr\}^{j_1k_1,j_2k_2}
\end{equation}
と書けることを示せ。

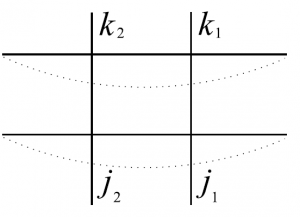
図18 $6$頂点模型の略記図

(2)水平方向・垂直方向が共に周期的境界条件であるとき、分配関数が
\begin{equation}
Z=\mathrm{tr}\bigl\{(\mathrm{tr}_0R_{02}R_{01})^2\bigr\}
\end{equation}
と書けることを示せ。

解答08

(1)$N=1$、$M=2$で水平方向だけ周期的境界条件が課されている場合（$\alpha=\alpha’$）、分配関数は
\[
(R_{02}R_{01})^{\alpha\alpha,j_1k_1,j_2k_2}=(\mathrm{tr}_0R_{02}R_{01})^{j_1k_1,j_2k_2}
\]
と書けていた。これと同様に考えれば、今の場合の分配関数は
\[
Z=\bigl\{(\mathrm{tr}_0R_{02}R_{01})^2\bigr\}^{j_1k_1,j_2k_2}
\]
となることが分かる。

(2)　(1)の結果に対して、垂直方向の周期的境界条件$j_1=k_1$と$j_2=k_2$を課すと、これはトレースの定義に他ならないので、
\[
Z=\mathrm{tr}\bigl\{(\mathrm{tr}_0R_{02}R_{01})^2\bigr\}
\]
と確かに書ける。

以上の議論は一般の$N$、$M$の場合に一般化出来る。

$R_{0j}\in\mathrm{End}(V_0\otimes V_1\otimes\cdots\otimes V_M)$を$L_j$と表記する。これをL 行列、またはLax 行列と呼ぶ。これは$2^{M+1}\times2^{M+1}$行列である。また、$T\in\mathrm{End}(V_0\otimes V_1\otimes\cdots\otimes V_M)$について$T\coloneqq L_ML_{M-1}\cdots L_1=R_{0M}R_{0M-1}\cdots R_{01}$と定義する。

問題09

$(T)^{\alpha\beta,h_1k_1,j_2k_2,\cdots,j_Mk_M}$は$1\times M$の正方格子上の自由境界条件における$6$頂点模型の分配関数であることを確かめよ。

解答09

今までの問題と同様に考えれば、求める分配関数は$(R_{0M}R_{0M-1}\cdots R_{01})^{\alpha\beta,j_1k_1,\cdots,j_Mk_M}$である。これは$T$の定義より、$(T)^{\alpha\beta,h_1k_1,j_2k_2,\cdots,j_Mk_M}$に他ならない。

$\mathcal{T}\in\mathrm{End}(V_1\otimes V_2\otimes\cdots\otimes V_M)$について$\mathcal{T}\coloneqq\mathrm{Tr}_0T$と定義する。これは$2^M\times2^M$行列である。これは転送行列に他ならない。

問題10

$N\times M$正方格子上の周期的境界条件における$6$頂点模型の分配関数$Z$は$Z=\mathrm{Tr}\mathcal{T}^N$であらわされることを示せ。

解答10

これも今までの問題と同様、問題7の分配関数についてトレース・部分トレースを取って、$N\times M$に拡張することを考えれば直ちに分かる。

$\mathcal{T}$の固有値を$\lambda_1,\cdots,\lambda_{2M}$とすると、分配関数$Z$は$Z=\lambda_1^N+\cdots+\lambda_{2M}^N$となる。