$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$

ベクトルはどのように変換するのか

「ベクトルは大きさと向きを持つ量である。」というベクトルの定義は、完全に満足出来るものではない。「”向き”の厳密な定義は何なのか？」という疑問が生ずるためである。

これは衒学的な疑問であると思うかもしれないが、我々はすぐに一見ベクトルのように見える派生物に遭遇して、本当にベクトルなのかどうかをはっきりさせなければならないことになるのである。

ベクトル解析に慣れていない初学者は、$3$つの成分があって、加算の下で正しく結合するものは何でもベクトルであると思いがちである。次のような問題を考えてみよう。

ここにフルーツバスケットがあって、その中に洋梨が$N_x$個、林檎が$N_y$個、バナナが$N_z$個あるとする。
では、このとき、$\bmn=N_x\hbx+N_y\hby+N_z\hbz$はベクトルと言えるだろうか？

確かにこれは$3$つの成分を持っている。そして洋梨が$M_x$個、林檎が$M_y$個、バナナが$M_z$個入っているような別のフルーツバスケットを用意して、$2$つのバスケットを足せば洋梨が$N_x+M_x$個、林檎が$N_y+M_y$個、バナナが$N_z+M_z$個になるから、ベクトルのような足し算が出来ている。

しかし、物理学者の言葉で言うと、これはベクトルではない。実際には向きを持っていないからである。では一体、何が悪いのだろうか？

答えは、$\bmn$は座標系を変えると正しく変換されないということである。

勿論我々は、位置を記述するために任意の座標系を用いることが出来るのだが、ある座標系と他の座標系の間にはベクトルの成分に対する特別な幾何学的変換則が存在する。

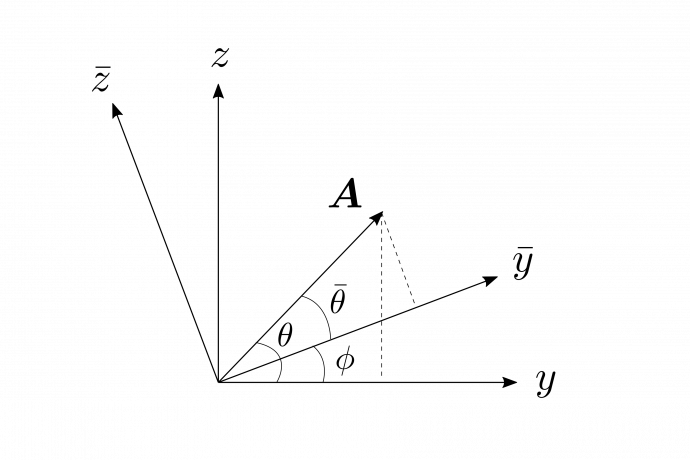
例えば、図1.15のように、$\bar{x},\bar{y},\bar{z}$座標系を、$x,y,z$座標系を$\phi$だけ回転させて、共通な軸を$x=\bar{x}$とした座標系として考えてみよう。

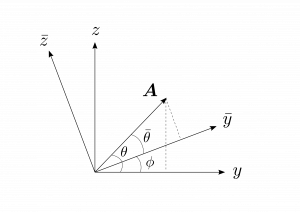
図1.15

このとき、$A_y$と$A_z$には

\[
A_y=A\cos{\theta},~A_z=A\sin{\theta}
\]

という関係がある。一方で、$\bar{A}_y$と$\bar{A}_z$には

\[
\left\{
\begin{array}{lcl}
\bar{A}_y&=&A\cos{\bar{\theta}}=A\cos{(\theta-\phi)}=A(\cos{\theta}\cos{\phi}+\sin{\theta}\sin{\phi})
&=&\cos{\phi}A_y+\sin{\phi}A_z\\
&&\\
\bar{A}_z&=&A\sin{\bar{\theta}}=A\sin{(\theta-\phi)}=A(\sin{\theta}\cos{\phi}-\cos{\theta}\sin{\phi})
&=&-\sin{\phi}A_y+\cos{\phi}A_z
\end{array}
\right.
\]

という関係がある。これらの結論を行列を用いてあらわすと、以下のように書くことが出来る。

\begin{equation}
\left(
\begin{array}{l}
\bar{A}_y\\
\bar{A}_z
\end{array}
\right)=\left(
\begin{array}{rr}
\cos{\phi}&\sin{\phi}\\
-\sin{\phi}&\cos{\phi}
\end{array}
\right)\left(
\begin{array}{l}
A_y\\
A_z
\end{array}
\right)\tag{29}
\end{equation}

より一般に、任意の軸に関する$3$次元の回転の変換則は次のような形を取る。

\begin{equation}
\left(
\begin{array}{l}
\bar{A}_x\\
\bar{A}_y\\
\bar{A}_z
\end{array}
\right)=\left(
\begin{array}{lll}
R_{xx}&R_{xy}&R_{xz}\\
R_{yx}&R_{yy}&R_{yz}\\
R_{zx}&R_{zy}&R_{zz}
\end{array}
\right)\left(
\begin{array}{l}
A_x\\
A_y\\
A_z
\end{array}
\right)\tag{30}
\end{equation}

よりコンパクトに、

\begin{equation}
\bar{A}_i=\sum_{j=1}^3R_{ij}A_j\tag{31}
\end{equation}

と書いても良い。但し、$1,2,3$の添字はそれぞれ$x,y,z$をあらわす。与えられた回転に関する行列$R$の要素は$x$軸の周りに回転させたときと同じように三角関数であらわすことが出来る。

では、$\bmn$の成分はこの方法で変換するだろうか？勿論、変換しない。

空間中の位置をあらわすためにどのような座標系を用いても、バスケットの中にはたくさんの林檎が存在し続けるだろう。違う座標軸を選んでも洋梨がバナナに変換されたりはしないが、$A_x$は$\bar{A}_y$に変換される。

つまり、正式には、座標系を変えたときに変位と同じように変換される$3$つの成分のセットのことをベクトルと言うのである。

いつものように、変位は全てのベクトルの振る舞いのモデルとなっている（もしあなたが数学的なことをやりたいなら、軸が方向と無関係で、$\hbx$、$\hby$、$\hbz$ではない基底ベクトルを持っている（実際には$3$次元以上の次元でも良い）、一般化されたベクトル空間について考えた方が良いかもしれない。これは線型代数学（linear algebra）の分野である。

しかし我々の議論では、12章での$4$次元時空以外は通常$3$次元空間を扱う。）。

ところで、$2$階のテンソル（tensor）は次の式のように、$9$個成分$T_{xx},T_{xy},T_{xz},T_{yx},\cdots,T_{zz}$を持っていて、$2$個の$R$の因子と共にに変換するような量である。

\begin{align}
\bar{T}_{xx}=&R_{xx}(R_{xx}T_{xx}+R_{xy}T_{xy}+R_{xz}T_{xz})\nonumber\\
&+R_{xy}(R_{xx}T_{yx}+R_{xy}T_{yy}+R_{xz}T_{yz})\nonumber\\
&+R_{xz}(R_{xx}T_{zx}+R_{xy}T_{zy}+R_{xz}T_{zz})+\cdots\nonumber
\end{align}

あるいは、よりコンパクトに

\begin{equation}
\bar{T}_{ij}=\sum_{k=1}^3\sum_{l=1}^3R_{ik}R_{jl}T_{kl}\tag{32}
\end{equation}

と書いても良い。

一般に、$n$階のテンソルは$n$個の添字と$3^n$個の成分を持っていて、$n$個の$R$の因子と共に変換する。この階層構造の下では、ベクトルは$1$階のテンソルで、スカラーは$0$階のテンソルであると言える（スカラーは座標系を変えても変化しない。特に、ベクトルの成分はスカラーではないが、ベクトルの大きさはスカラーである。）。