\[
\def\bm#1{{\boldsymbol{#1}}}
\]
この記事では大学院入試対策として有効な演習について数回にわたって行っていきたいと思います。
演習は問題→解説の順番で行います。
初回となる今回は古典力学のKepler 問題について扱います。
1.1 問題
[問題1] 中心力を受けて運動する物体の軌跡は平面内に限られるということを示せ(Kepler の第2法則)。
[問題2] 中心力ポテンシャル$U(r)$のもとで、質量$m$の物体の運動を極座標$(r,\phi)$を用いてあらわすことにする。
(1)運動エネルギーが以下の式で与えられることを示せ。
\[
K=\frac{1}{2}\{\dot{r}^2+(r\dot{\phi})^2\}
\]
(2)Euler-Lagrange の運動方程式を求めよ。
(3)この系の力学的エネルギーが保存することを示せ。
[問題3] 原点に置かれた質量$M(M\gg m)$の物体による重力場$U(r)=-\displaystyle\frac{GMm}{r}$を考える。
(1)問題2で求めた運動方程式において$r^2\dot{\phi}=L$($L$は定数)とおくことにより
\[
\frac{d^2}{d\phi^2}\left(\frac{1}{r}\right)+\frac{1}{r}=\frac{GM}{L^2}
\]
が成り立つことを示せ。
(2)前問の運動方程式の解は$A$、$B$を定数として
\[
\frac{1}{r}=A\cos{\phi}+B\sin{\phi}+\frac{GM}{L^2}
\]
で与えられることを示せ。また、$\phi=0$のときに$r$が最小になると考えて
\[
\left\{
\begin{array}{l}
\left[\displaystyle\frac{d}{d\phi}\left(\displaystyle\frac{1}{r}\right)\right]_{\phi=0}=B=0\\
\\
\left[\displaystyle\frac{d^2}{d\phi^2}\left(\displaystyle\frac{1}{r}\right)\right]_{\phi=0}=-A<0
\end{array}
\right.
\]
とおくことにより$r$が以下のように得られることを示せ。また、$e$、$l$の定義を与えよ。
\[
r=\frac{l}{1+e\cos{\phi}}
\]
(3)この物体の軌跡を$e=0$、$0<e<1$、$e=1$、$e>1$のそれぞれの場合について図示せよ(Kepler の第1法則)。
[問題4] この系の力学的エネルギーが
\[
E=\frac{m}{2}\dot{r}^2-\frac{GMm}{r}+\frac{mL^2}{2r^2}
\]
とあらわされることを示し、動径方向の有効ポテンシャル
\[
U_{\mathrm{eff}}=-\frac{GMm}{r}+\frac{mL^2}{2r^2}
\]
の$r$依存性を調べて、$E$の大小による軌跡の違いを説明せよ。
[問題5]物体が楕円軌道を描くとき、楕円の長軸の長さを$2a$として、周期$T$との間の関係$T^2\propto a^3$を示せ(Kepler の第3法則)。また、太陽系の惑星の$T$、$a$を調べてこの法則を検証せよ。
1.2 解答
[問題1]
「中心力を受けて運動する物体の軌跡は平面内に限られる」という事を示すには、
\[
\displaystyle\frac{d\mathbf{L}}{dt}=\displaystyle\frac{d}{dt}(\mathbf{r}\times m\mathbf{\dot{r}})=\mathbf{\dot{r}}\times m\mathbf{\dot{r}}+\mathbf{r}\times m\mathbf{\ddot{r}}=\mathbf{0}\nonumber
\]
が示せれば良い。何故なら上の式が成り立つとき、角運動量ベクトルが常に一定の方向を向くため特定の平面上に運動量ベクトルが存在するからである。さて、外積の定義より第1項は${0}$なので結局、$\mathbf{r}\times\mathbf{\ddot{r}}=\mathbf{0}$が言えれば良いことになる。中心力が働くときの運動方程式を用いて、
\begin{eqnarray}
\mathbf{r}\times m\mathbf{\ddot{r}}=\mathbf{r}\times \left(-m\displaystyle\frac{dU(r)}{dr}\frac{\mathbf{r}}{r}\right)=\mathbf{0}\nonumber
\end{eqnarray}
よって題意は示された。
[問題2]
(1) 2次元極座標$(r,\phi)$の定義及びそれを時間微分した式
\begin{eqnarray}
{
\left(
\begin{array}{l}
x\\
y
\end{array}
\right)=
\left(
\begin{array}{l}
r\cos{\phi}\\
r\sin{\phi}
\end{array}
\right) 、
\left(
\begin{array}{l}
\dot{x}\\
\dot{y}
\end{array}
\right)=
\left(
\begin{array}{l}
\dot{r}\cos{\phi}-r\dot{\phi}\sin{\phi}\\
\dot{r}\sin{\phi}+r\dot{\phi}\cos{\phi}
\end{array}
\right)}\nonumber
\end{eqnarray}
より考えている系の運動エネルギーは、以下のように計算できる。よって題意は示された。
\begin{eqnarray}
{
K=\displaystyle\frac{m}{2}(\dot{x}^2+\dot{y}^2)=\displaystyle\frac{m}{2}\{\dot{r}^2+(r\dot{\phi})^2\}}\nonumber
\end{eqnarray}
(2) 問題2(1)で求めた運動エネルギーを用いれば考えている系のLagrangian は、
\begin{eqnarray}
{\mathcal{L}=\displaystyle\frac{m}{2}\{\dot{r}^2+(r\dot{\phi})^2\}-U(r)
}\nonumber
\end{eqnarray}
と求まる。これより、この系のEuler-Lagrange の運動方程式は以下のように書ける。
\begin{eqnarray}
{
\left\{
\begin{array}{l}
\displaystyle\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{r}}\right)-\displaystyle\frac{\partial\mathcal{L}}{\partial r}=m\ddot{r}-\left\{mr\dot{\phi}^2-\displaystyle\frac{dU(r)}{dr}\right\}=0\\
\\
\displaystyle\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{\phi}}\right)-\displaystyle\frac{\partial\mathcal{L}}{\partial \phi}=\displaystyle\frac{d}{dt}(mr^2\dot{\phi})-0=0
\end{array}
\right.}\nonumber
\end{eqnarray}
よって題意は示された。
(3) Lagrangian が時間に陽に依存していないので自明。
よって題意は示された。
[問題3]
(1) 問題2(2)で得られたEuler-Lagrange の運動方程式に$U(r)$と$r^2\dot{\theta}=L$を代入して、
\begin{eqnarray}
{\ddot{r}=\displaystyle\frac{L^2}{r^3}-\frac{GM}{r^2}}\nonumber
\end{eqnarray}
が得られる。ここで$r$を$\phi$で微分する形に書き換えることを目指すと、
\begin{eqnarray}
{\dot{r}=\frac{d\phi}{dt}\frac{dr}{d\phi}=\frac{L}{r^2}\frac{dr}{d\phi}=-L\frac{d}{d\phi}\left(\frac{1}{r}\right)}\nonumber
\end{eqnarray}
\begin{eqnarray}
{\ddot{r}=-L\frac{d\phi}{dt}\frac{d}{d\phi}\left\{\frac{d}{d\phi}\left(\frac{1}{r}\right)\right\}=-\frac{L^2}{r^2}\frac{d^2}{d\phi^2}\left(\frac{1}{r}\right)}\nonumber
\end{eqnarray}
が得られる。よってEuler-Lagrange の運動方程式は、
\begin{eqnarray}
{-\displaystyle\frac{L^2}{r^2}\left\{\frac{d^2}{d\phi^2}\left(\frac{1}{r}\right)+\frac{1}{r}\right\}=-\frac{GM}{r^2}}\nonumber
\end{eqnarray}
と書き換えられる。この式を両辺$-\displaystyle\frac{L^2}{r^2}$で割れば所望の式を得る。
(2) $u=\displaystyle\frac{1}{r}-\frac{GM}{L^2}$とおくと、単振動の微分方程式の形、
\begin{eqnarray}
{\displaystyle\frac{d^2u}{d\phi^2}+u=0}\nonumber
\end{eqnarray}
が得られるから、元の形に戻せば解は任意定数$A,B$を用いて以下のように書ける。
\begin{eqnarray}
{\displaystyle\frac{1}{r}=A\cos{\phi}+B\sin{\phi}+\frac{GM}{L^2}}\nonumber
\end{eqnarray}
問題文の初期条件に従えば右辺第二項が$0$になる。右辺第1項・第3項は共に正の値を取るので$0$で割っても良いから、
\begin{eqnarray}
{r=\displaystyle\frac{1}{\displaystyle\frac{GM}{L^2}+A\cos{\phi}}=\frac{\displaystyle\frac{L^2}{GM}}{1+\displaystyle\frac{AL^2}{GM}\cos{\phi}}=\frac{l}{1+e\cos{\phi}}}\nonumber
\end{eqnarray}
従って$l、e$はそれぞれ$l=\displaystyle\frac{L^2}{GM}、e=\displaystyle\frac{AL^2}{GM}$となる。
(3) $e = 0$,$0 < e < 1$,$e = 1$,$e > 1$ はそれぞれ円軌道、楕円軌道、放物線軌道、双曲線軌道を表している。それぞれの軌道は下図の通り。
$e = 0$,$0 < e < 1$,$e = 1$,$e > 1$ に対応した物体の軌道

[問題4]
問題2(1)で得た運動エネルギーの式と問題3で与えられたポテンシャルエネルギーの式を用いて得られた力学的エネルギーの式において$r^2\dot{\phi}=L$を利用して$\dot{\phi}$を消去すれば、
\begin{eqnarray}
{E=\displaystyle\frac{m}{2}\dot{r}^2-\frac{GMm}{r}+\frac{mL^2}{2r^2}}\nonumber
\end{eqnarray}
が直ちに得られる。さて、こうすることによって力学的エネルギーの第2・3項を$r$のみの関数として表すことが出来るから、これを有効ポテンシャル$U_{\mathrm{eff}}(r)$と定義する。すなわち、
\begin{eqnarray}
{U_{\mathrm{eff}}(r)=-\displaystyle\frac{GMm}{r}+\frac{mL^2}{2r^2}}\nonumber
\end{eqnarray}
である。この$U_{\mathrm{eff}}(r)$について$\displaystyle\frac{dU_{\mathrm{eff}}(r)}{dr}=0$及び$\displaystyle\frac{d^2U_{\mathrm{eff}}(r)}{dr^2}=0$を解けば、極小点、力学的エネルギーの極小値と変曲点はそれぞれ以下のように求まる。
$r=\displaystyle\frac{L^2}{GM}~(極小点)$ 、
$E=-\dfrac{G^2M^2m}{2L^2}<0~(力学的エネルギーの極小値)$ 、
$r=\displaystyle\frac{3L^2}{2GM}~(変曲点)$。
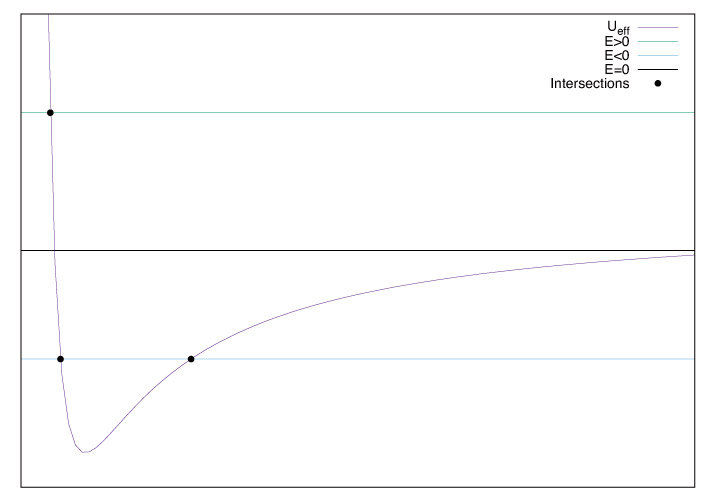
これらより、有効ポテンシャル$U_{\mathrm{eff}}(r)$の概形は下図の通り。
$E=(定数)$の直線を$x$軸に平行に引いたとき、$E$の直線と$U_{\mathrm{eff}}(r)$の差分が運動エネルギーに相当する(但し、運動エネルギーは正の値を取る)。
$E\geq 0$のとき、$E$と$U_{\mathrm{eff}}(r)$の交点は1点であり、この点において運動エネルギーが$0$となる。これは動径方向の速度が$0$であることを意味するから、無限遠から飛来した物体はこの転回点まで接近した後に無限遠へ再び飛び去ることが分かる。
$E<0$のとき、$E$と$U_{\mathrm{eff}}(r)$の交点は2点であり、引力中心と物体間の距離はこの2点の転回点の間を増減する。つまり、物体は引力中心から最も離れた点と最も接近した点を通る周回軌道を描く。これらの点をそれぞれ遠日点、近日点という。
$E>0$、$E=0$、$E<0$はそれぞれ双曲線軌道、放物線軌道、楕円軌道に対応しており特に$E$が極小値を取るとき円軌道となる。
図 2 有効ポテンシャル $U_{\mathrm{eff}}(r)$の $r $依存性と力学的エネルギーの関係
[問題5]
物体が楕円軌道を描くとき、面積速度と公転周期の積は物体の描く楕円軌道の面積であるから、楕円軌道の長軸と短軸の長さをそれぞれ$2a$、$2b$とすると以下の式が一般に成り立つ。
\begin{eqnarray}
{\displaystyle\frac{LT}{2}=\pi ab}\nonumber
\end{eqnarray}
楕円の性質より$a$、$b$には$a=\displaystyle\frac{l}{1-e^2}$、$b=\displaystyle\frac{l}{\sqrt{1-e^2}}=a\sqrt{1-e^2}$という関係がある。
よってこれらより、問題3(2)で考えた$l$の定義を用いれば、
\begin{eqnarray}
{T^2=\left(\displaystyle\frac{2\pi ab}{L}\right)^2=\displaystyle\frac{4\pi^2 a^4}{L^2(1-e^2)}=\frac{4\pi^2}{GM}a^3}\nonumber
\end{eqnarray}
これはKepler の第3法則に他ならない。
次に参考文献{[4]}を用いて各惑星の$\displaystyle\frac{T^2}{a^3}$の値を計算した。その値は下表の通り。
この表から分かるように、各惑星の離心率の値に依らずほぼ一定値をとっている。
Kepler の第3法則の検証
| 惑星 | 軌道長半径$a$(天文単位) | 対恒星公転周期$T$(Julius 年) | $T^2/a^3$ | 離心率$e$ |
| 水星 | 0.3781 | 0.24085 | 1.0731 | 0.2056 |
| 金星 | 0.7233 | 0.61520 | 1.0014 | 0.0068 |
| 地球 | 1.0000 | 1.00002 | 1.0000 | 0.0167 |
| 火星 | 1.5237 | 1.88085 | 1.0000 | 0.0934 |
| 木星 | 5.2026 | 11.8620 | 0.9992 | 0.0485 |
| 土星 | 9.5549 | 29.4572 | 0.9947 | 0.0554 |
| 天王星 | 19.2184 | 84.0205 | 0.9945 | 0.0463 |
| 海王星 | 30.1104 | 164.7701 | 0.9945 | 0.0090 |
第2回目は剛体の運動について紹介しますので、こちらからご覧ください。
参考文献
[1] 石井靖,藤原毅夫『工学基礎 力学』,数理工学社,2016
[2] 篠本滋,坂口英継『基幹講座物理学 力学』,東京図書,2013
[3] ランダウ,リフシッツ著,広重徹,水戸巌訳,『力学』,2014
[4] 国立天文台,『理科年表 平成 29 年』,丸善出版,2016