$\def\bm#1{{\boldsymbol{#1}}}$

$\def\coloneqq{{:=}}$

第２回では剛体の運動(対称な独楽)について扱いましたが、今回は電磁気学の輻射の問題です！

3.1　問題

[問題1] 時間的に変わる電荷分布・電流分布が作るポテンシャルは

\[
\left\{
\begin{array}{l}
\phi(\bm{r},t)=\dfrac{1}{4\pi\varepsilon_0}\int d\bm{r}’~\dfrac{\rho(\bm{r},t-\frac{|\bm{r}-\bm{r}’|}{c})}{|\bm{r}-\bm{r}’|}\\
\\
{A}(\bm{r},t)=\dfrac{\mu_0}{4\pi}\int d\bm{r}’~\dfrac{\bm{i}(\bm{r},t-\frac{|\bm{r}-\bm{r}’|}{c})}{|\bm{r}-\bm{r}’|}
\end{array}
\right.
\]

で与えられることを示せ（遅延ポテンシャル）。また、電荷保存則
\[
\dfrac{\partial\rho}{\partial t}+\nabla\cdot\bm{i}=0
\]
が満たされていれば、Lorenz 条件が自然に成立することを示せ。

[問題2] $(0、0、\pm a)$に$\pm q$の点電荷が置かれており、このとき$q$が$q=q_0\cos{\omega t}=\mathrm{Re}(q_0\mathrm{e}^{-i\omega t})$と変化する双極子を考える。このとき、$2$次元には$\bm{i}=(dq/dt)(0、0、1)$の電流が生じている。この振動する双極子が点$\bm{r}$に作る場$\phi$、$\bm{A}$を求めよ。但し、$\omega =ck$、$ka\ll1$、$a\ll r=|\bm{r}|$とする。

また、$kr\gg1$（輻射領域）における電場$\bm{E}$、磁場$\bm{H}$、及びPoynting ベクトル$\bm{S}=\bm{E}\times\bm{H}$の時間平均を求め、放出される電磁波のエネルギーの方向分布（指向性）を議論せよ。

[問題3] 半径$a$の円環を周波数$\omega$の高周波電流が流れる場合、円環から遠く離れた点$\bm{r}(|\bm{r}|\gg a)$に作られる場$\phi$、$\bm{A}$を求めよ。問題2と同様、$kr\gg1$（輻射領域）における電場$\bm{E}$、磁場$\bm{H}$、及びPoynting ベクトル$\bm{S}=\bm{E}\times\bm{H}$の時間平均を求め、放出される電磁波のエネルギーの方向分布（指向性）を議論せよ。但し、$ka\ll1$である。

[問題4] 問題2、問題3において$kr\ll1(r\gg a)$の非輻射領域に作られる電磁場を求め、その特徴を議論せよ。これは、$\omega=ck$を考慮すれば、$(r/c)\ll\omega^{-1}$、すなわち、原点に置かれた源からの影響が観測点に伝わるのに要する時間に比べて、振動の周期が長い場合に相当する。

3.2　演習問題解答

[問題1]
$\phi$、$\bm{A}$の方程式はいずれも非斉次の波動方程式
\begin{eqnarray}
{\Delta F({r},t)-\displaystyle\frac{1}{c^2}\frac{\partial^2F({r}、t)}{\partial t^2}=f({r},t)
}
\end{eqnarray}
の形をしている。ここではGreen 関数を用いてその解を構成することを考える。時間$t$に対してはFourier 変換
\begin{eqnarray}
{F(\bm{r},t)=\displaystyle\frac{1}{\sqrt{2\pi}}\int^{\infty}_{-\infty}\hat{F}(\bm{r}、\omega)\mathrm{e}^{-i\omega t}d\omega 、　f(\bm{r},t)=\displaystyle\frac{1}{\sqrt{2\pi}}\int^{\infty}_{-\infty}\hat{f}(\bm{r}、\omega)\mathrm{e}^{-i\omega t}dt
}\nonumber
\end{eqnarray}
を用いて色々な振動数を持つ単振動の合成として表す。但しFourier 逆変換はそれぞれ
\begin{eqnarray}
{\hat{F}(\bm{r},\omega)=\displaystyle\frac{1}{\sqrt{2\pi}}\int^{\infty}_{-\infty}F(\bm{r},t)\mathrm{e}^{i\omega t}d\omega 、　\hat{f}(\bm{r},\omega)=\displaystyle\frac{1}{\sqrt{2\pi}}\int^{\infty}_{-\infty}f(\bm{r},t)\mathrm{e}^{i\omega t}dt
}\nonumber
\end{eqnarray}
である。こうすると式(1)は
\begin{eqnarray}
(\Delta+k_0^2)\hat{F}({r},\omega)=\hat{f}(\bm{r},\omega)
\end{eqnarray}
と書き直すことが出来る。この方程式に対して
\begin{eqnarray}
(\Delta_{\bm{r}}+k_0^2)G_k(\bm{r},\bm{r}’)=\delta(\bm{r}-\bm{r}’)
\end{eqnarray}
を満たす$G_k({r}、{r}’)$を3次元空間のGreen 関数という。これを用いれば
\begin{eqnarray}
{\hat{F}(\bm{r},\omega)=\int G_k(\bm{r},\bm{r}’)\hat{f}(\bm{r}’,\omega)dV’
}\nonumber
\end{eqnarray}
によって式(2)の解を構成することが出来る。但し、$\Delta_{\bm{r}}$は$\bm{r}$に関するLaplacian を意味している。式(1)の解は逆Fourier 変換によって
\begin{eqnarray}
{F(\bm{r},t)=\int dV’\int^{\infty}_{-\infty}dt’f({r}’,t’)\frac{1}{2\pi}\int^{\infty}_{-\infty}G_k(\bm{r},\bm{r}’)\mathrm{e}^{i\omega(t-t’)}d\omega
}\nonumber
\end{eqnarray}
と表される。これを
\begin{eqnarray}
{G(\bm{r},t:\bm{r}’,t’)=\frac{1}{2\pi}\int^{\infty}_{-\infty}G_k(\bm{r},\bm{r}’)\mathrm{e}^{i\omega(t’-t)}d\omega
}
\end{eqnarray}
を用いて
\begin{eqnarray}
{F(\bm{r},t)=\int G(\bm{r},t:\bm{r}’,t’)f(\bm{r}’,t)dV’dt’
}
\end{eqnarray}
と表す。これらより、$G(\bm{r},t:\bm{r}’,t’)$は以下の方程式を満たすことが分かる。
\begin{eqnarray}
{\left(\Delta_{\bm{r}}-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)G=\delta(\bm{r}-\bm{r}’)\delta(t-t’)
}\nonumber
\end{eqnarray}
これを満たす$G(\bm{r},t:\bm{r}’,t’)$を4次元空間のGreen 関数と言い、それを用いれば式(1)の解が式(5)によって構成されることになる。Green 関数$G_k$は境界条件ごとに適切なものを選ばなければならない。最も簡単な場合として境界を持たない場合を考えると球対称性より$R$にのみ依存することになるので、このときの極座標$(R,\theta,\varphi)$におけるLaplacian は$R$のみによる偏微分項だけ考えればいい。結局、式(3)は
\begin{eqnarray}
{\left(\frac{d^2}{dR^2}+k_0^2\right)RG_k(R)=R\delta(\bm{r}-\bm{r}’)=0
}\nonumber
\end{eqnarray}
となる。これを満たす独立な2つの解は
\begin{eqnarray}
{RG^{(\pm)}_k(R)=C_\pm\mathrm{e}^{ikR}
}\nonumber
\end{eqnarray}
であり、定数$C_{\pm}$は式(3)から決まり、$C_{\pm}=-\displaystyle\frac{1}{4\pi}$と求まる。このうち$G^{(+)}_k(R)$を採用し、式(1)の右辺を0に置き換えてできる斉次方程式の解が0であるとすれば
\begin{eqnarray}
{F(\bm{r},t)=-\int \frac{f(\bm{r}’,t-R/c)}{4\pi R}dV’
}\nonumber
\end{eqnarray}
を得るからここに適切な関数を代入することで所望の式が得られる。\\

後半の問題に関しては、Lorenz 条件と特殊相対性理論の関係について考えれば直ちに分かる。あるいはJefimenko 方程式との関係性を考える方法もある。Jefimenko 方程式について記述されている本としては参考文献[2]などがある。

[問題2]
今、対称性より原点から位置ベクトル$\bm{r}$で結ばれるようなある点が$y-z$平面上にあるとして議論しても一般性を失わない。これを考慮して下図のように座標系と変数を定める。

電気双極子と考えている点の概略図

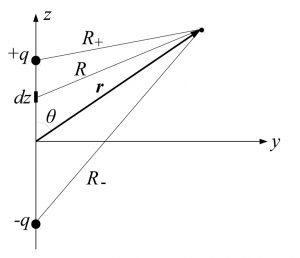
以下、考える電荷を$q(t)=q_0\cos{\omega t}$とおくことにする。今、図1から明らかにスカラー遅延ポテンシャル$\phi(\bm{r},t)$は
\begin{eqnarray}
{\phi(\bm{r},t)=\displaystyle\frac{1}{4\pi\varepsilon_0}\left\{\frac{q_0\cos{(\omega t-kR_+)}}{R_+}-\frac{q_0\cos{(\omega t-kR_-)}}{R_-}\right\}
}\nonumber
\end{eqnarray}
である。但し$R_\pm$は余弦定理より$R_\pm=\sqrt{r^2\mp2ra\cos{\theta}+a^2}$で与えられる。

さて、$a\ll r$及び$ka\ll1$より$R_\pm\simeq r\left(1\mp\displaystyle\frac{a}{r}\cos{\theta}\right)\rightarrow\displaystyle\frac{1}{R_\pm}=\frac{1}{r}\left(1\pm\frac{a}{r}\cos{\theta}\right)$及び$\cos{(\omega t-kR_\pm)}\simeq\cos{\{(\omega t-kr)+ka\cos{\theta}\}}=\cos(\omega t -kr)\cos{(ka\cos{\theta})}\\\mp\sin(\omega t -kr)\sin{(ka\cos{\theta})}\simeq\cos{(\omega t-kr)}\mp ka\cos{\theta}\sin{(\omega t-kr)}$を得る。

これらを代入して遅延スカラーポテンシャルは
\begin{eqnarray}
{\phi(\bm{r},t)\simeq\displaystyle\frac{p_0\cos{\theta}}{4\pi \varepsilon_0 r}\left\{-\frac{\omega}{c}\sin{(\omega t-kr)}+\frac{1}{r}\cos{(\omega t-kr)}\right\}}
\end{eqnarray}
と求められる。但し、$p_0\coloneqq2q_0a$である。特に$kr\gg1$のとき、
\begin{eqnarray}
{\phi(\bm{r},t)\simeq-\displaystyle\frac{p_0\omega}{4\pi \varepsilon_0c}\left(\frac{\cos{\theta}}{r}\right)\sin{(\omega t-kr)}}\nonumber
\end{eqnarray}
と近似できる。

一方、ベクトル遅延ポテンシャル$\bm{A}({r},t)$は図1より
\begin{eqnarray}
{\bm{A}({r},t)=\displaystyle\frac{\mu_0}{4\pi}\int^{a}_{-a} \frac{-q_0\omega\sin{(\omega t-kR)}}{R}\bm{e}_zdz
}\nonumber
\end{eqnarray}
と書ける。ここで先に得た近似式を代入して(但し、$kr\gg1$に基づいた近似は用いていないことに注意)、1次以上の項を省略すれば遅延ベクトルポテンシャルは
\begin{eqnarray}
{{A}(\bm{r},t)\simeq-\displaystyle\frac{\mu_0p_0\omega}{4\pi r}\sin{(\omega t-kr)}\bm{e}_zdz
}
\end{eqnarray}
と求められる。これらを利用すれば電場、磁束密度、Poynting ベクトル及びその時間平均はそれぞれ順に以下のように求まる。電磁波のエネルギーは動径方向に放出される。

\begin{eqnarray}
\left\{
\begin{array}{l}
\boldsymbol{E}(\boldsymbol{r},t)=-\nabla\phi-\displaystyle\frac{\partial \boldsymbol{A}}{\partial t}=-\frac{\mu_0p_0\omega^2}{4\pi}\left(\frac{\sin{\theta}}{r}\right)\cos{(\omega t-kr)}\boldsymbol{e}_{\theta}\\
\\
\boldsymbol{B}(\boldsymbol{r},t)=\nabla\times\boldsymbol{A}=-\displaystyle\frac{\mu_0p_0\omega^2}{4\pi c}\left(\frac{\sin{\theta}}{r}\right)\cos{(\omega t-kr)}\boldsymbol{e}_{\varphi}\\
\\
\boldsymbol{S}(\boldsymbol{r},t)=\displaystyle\frac{1}{\mu_0}\boldsymbol{E}\times\boldsymbol{B}=\frac{\mu_0}{c}\left\{\frac{p_0\omega^2}{4\pi}\left(\frac{\sin{\theta}}{r}\right)\cos{(\omega t-kr)}\right\}^2\boldsymbol{e}_r\\
\\
\langle\boldsymbol{S}\rangle=\left(\displaystyle\frac{\mu_0p_0^2\omega^4}{32\pi^2c}\right)\displaystyle\frac{\sin^2{\theta}}{r^2}\boldsymbol{e}_r\\
~
\end{array}
\right.\nonumber
\end{eqnarray}

また、これより全輻射エネルギー$\langle P \rangle_{\mathrm{electric}}$は$\langle S\rangle\coloneqq\langle {S}\rangle\cdot\bm{e}_r$を用いて
\begin{eqnarray}
{\langle P \rangle_{\mathrm{electric}}=\displaystyle\int^{\pi}_{0}2\pi\langle S\rangle r^2\sin{\theta}d\theta=\frac{\mu_0p_0^2\omega^4}{12\pi c}}\nonumber
\end{eqnarray}
と求まる。

[問題3]

今、考えているのは円形回路なので対称性より原点から位置ベクトル$\bm{r}$で結ばれるようなある点が$x-z$平面上にあるとして議論しても一般性を失わない。これを考慮して下図のように座標系と変数を定める。但し、$\psi$は$\bm{a}$と$\bm{r}$のなす角である。

円形回路と考えている点の概略図

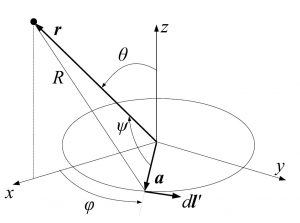
以下、考える電流を$I(t)=I_0\cos{\omega t}$とおくことにする。今、問題の設定から明らかにスカラー遅延ポテンシャル$\phi(\bm{r},t)$は0である。一方、ベクトル遅延ポテンシャル$\bm{A}({r}、t)$は
\begin{eqnarray}
{\bm{A}(\bm{r},t)=\displaystyle\frac{\mu_0}{4\pi}\int \frac{I_0\cos{(\omega t-kR)}}{R}d{l}’=\frac{\mu_0I_0a}{4\pi}\int^{2\pi}_{0} \frac{\cos{(\omega t-kR)}}{R}\cos{\varphi}\bm{e}_yd\varphi
}\nonumber
\end{eqnarray}
と書ける。ここで先に課した、考えている点が$x-z$平面上にあるという条件より、$x$成分が自明に0となることを計算に用いた。今、$\bm{a}$と$\bm{r}$の定義及び$\bm{a}\cdot\bm{r}$から$\cos{\psi}=\sin{\theta}\cos{\varphi}$が導けることを利用すれば余弦定理より$R=\sqrt{r^2+a^2-2ra\sin{\theta}\cos{\varphi}}$が得られる。

さて、$a\ll r$及び$ka\ll1$より$R\simeq r\left(1-\displaystyle\frac{a}{r}\sin{\theta}\cos{\varphi}\right)\rightarrow\displaystyle\frac{1}{R}=\frac{1}{r}\left(1+\frac{a}{r}\sin{\theta}\cos{\varphi}\right)$及び$\cos{(\omega t-kR)}\simeq\cos{(\omega t-kr)+ka\sin{\theta}\cos{\varphi}}=\cos(\omega t -kr)+\cos{(ka\sin{\theta}\cos{\varphi})}-\sin(\omega t -kr)+\sin{(ka\sin{\theta}\cos{\varphi})}\simeq\cos{(\omega t-kr)}-ka\sin{\theta}\cos{\varphi}\sin{(\omega t-kr)}$を得る。

これらを代入して2次以上の項を省略すれば遅延ベクトルポテンシャルは
\begin{eqnarray}
{\bm{A}(\bm{r},t)\simeq\displaystyle\frac{\mu_0I_0a}{4\pi r}{e}_y\int^{2\pi}_{0} \biggr\{\cos{(\omega t-kr)}+a\sin{\theta}\cos{\varphi}\times\biggl(\displaystyle\frac{1}{r}\cos{(\omega t-kr)}}\nonumber\\
&-&k\sin{(\omega t-kr)}\biggr)\biggr\}\cos{\varphi}d\varphi=\displaystyle\frac{\mu_0m_0}{4\pi}\left(\frac{\sin{\theta}}{r}\right)\biggl\{\frac{1}{r}\cos{(\omega t-kr)}-k\sin{(\omega t-kr)}\biggr\}\bm{e}_{\varphi}　(8)\nonumber
\end{eqnarray}
と求められる。但し、$m_0\pi a^2I_0$である。\\

特に$kr\gg1$のとき、第1項は無視できるからこのときの遅延ベクトルポテンシャルは
\begin{eqnarray}
{\bm{A}(\bm{r},t)\simeq-\displaystyle\frac{\mu_0m_0\omega}{4\pi c}\left(\frac{\sin{\theta}}{r}\right)\sin{(\omega t-kr)}\bm{e}_{\varphi}}\nonumber
\end{eqnarray}
と求められる。これを利用すれば電場、磁束密度、Poynting ベクトル及びその時間平均はそれぞれ順に以下のように求まる。電磁波のエネルギーは動径方向に放出される。
\begin{eqnarray}
\left\{
\begin{array}{l}
\bm{E}(\bm{r},t)=-\displaystyle\frac{\partial {A}}{\partial t}=\frac{\mu_0m_0\omega^2}{4\pi c}\left(\frac{\sin{\theta}}{r}\right)\cos{(\omega t-kr)}\bm{e}_{\varphi}\\
\\
\bm{B}(\bm{r},t)=\nabla\times{A}=-\displaystyle\frac{\mu_0m_0\omega^2}{4\pi c}\left(\frac{\sin{\theta}}{r}\right)\cos{(\omega t-kr)}\bm{e}_{\theta}\\
\\
\bm{S}(\bm{r},t)=\displaystyle\frac{1}{\mu_0}{E}\times{B}=\frac{\mu_0}{c}\left\{\frac{m_0\omega^2}{4\pi c}\left(\frac{\sin{\theta}}{r}\right)\cos{(\omega t-kr)}\right\}^2\bm{e}_r\\
\\
\langle\bm{S}\rangle=\left(\displaystyle\frac{\mu_0m_0^2\omega^4}{32\pi^2c^3}\right)\displaystyle\frac{\sin^2{\theta}}{r^2}\bm{e}_r\\
~
\end{array}
\right.\nonumber
\end{eqnarray}
また、これより全輻射エネルギー$\langle P \rangle_{\mathrm{magnetic}}$は$\langle S\rangle\coloneqq\langle \bm{S}\rangle\cdot\bm{e}_r$を用いて
\begin{eqnarray}
{\langle P \rangle_{\mathrm{magnetic}}=\displaystyle\int^{\pi}_{0}2\pi\langle S\rangle r^2\sin{\theta}d\theta=\frac{\mu_0m_0^2\omega^4}{12\pi c^3}}\nonumber
\end{eqnarray}
と求まる。これと問題2で導いた$\langle P \rangle_{\mathrm{electric}}$より
\begin{eqnarray}
{\displaystyle\frac{\langle P \rangle_{\mathrm{magnetic}}}{\langle P \rangle_{\mathrm{electric}}}=\left(\displaystyle\frac{m_0}{p_0c}\right)^2\rightarrow\biggl(\displaystyle\frac{\omega a}{c}\biggr)^2　(~(問題2における2a)=(問題3における~\pi a)~)}\nonumber
\end{eqnarray}
問題の条件よりこの値は非常に小さい。これは本問題のように電気的な寄与がないという設定に限り磁気双極子輻射があらわになることを意味している。

[問題4]
定常状態における電気双極子モーメント及び磁気双極子モーメントをそれぞれ
$\bm{p}(t) p_0\bm{e}_z$、$\bm{m}(t) m_0\bm{e}_z$と定義する。

$kr\ll 1$の条件の下で、問題2における遅延スカラーポテンシャル、遅延ベクトルポテンシャル、電場、磁束密度は式(6)及び式(7)よりそれぞれ
\begin{eqnarray}
{
\left\{
\begin{array}{l}
\phi(\bm{r},t)=\dfrac{1}{4\pi\varepsilon_0}\dfrac{\bm{p}\cdot\bm{r}}{r^3}\\
\\
\bm{A}(\bm{r},t)=\bm{0}\\
\\
\bm{E}(\bm{r},t)=\dfrac{1}{4\pi\varepsilon_0}\left\{\dfrac{3(\bm{p}\cdot\bm{r})}{r^5}\bm{r}-\dfrac{1}{r^3}\bm{p}\right\}\\
\\
\bm{B}(\bm{r},t)=\bm{0}\\
~
\end{array}
\right.}\nonumber
\end{eqnarray}
となる。これは定常状態における電気双極子が与える結果に等しい。

$kr\ll1$の条件の下で、問題3における遅延スカラーポテンシャル、遅延ベクトルポテンシャル、電場、磁束密度は式(8)及び$\phi(\bm{r},t)=0$よりそれぞれ
\begin{eqnarray}
{
\left\{
\begin{array}{l}
\phi(\bm{r},t)=0\\
\\
\bm{A}(\bm{r},t)=\displaystyle\frac{\mu_0}{4\pi}\frac{\bm{m}\times\bm{r}}{r^2}\\
\\
\bm{E}(\bm{r},t)=\bm{0}\\
\\
\bm{B}(\bm{r},t)=\displaystyle\frac{\mu_0}{4\pi}\left\{\frac{3(\bm{m}\cdot\bm{r})}{r^5}\bm{r}-\frac{1}{r^3}\bm{m}\right\}+\mu_0\delta(\bm{r})\bm{m}\\
~
\end{array}
\right.}\nonumber
\end{eqnarray}
となる。これは定常状態における磁気双極子が与える結果に等しい。

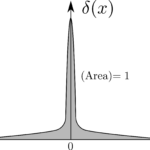
但し、$\delta(\bm{r})$はDirac のデルタ関数である。また、勝手な3次元ベクトル$\bm{X}$、$\bm{Y}$と位置ベクトル$\bm{r}$に成り立つ以下の公式を用いた。
\begin{eqnarray}
{
\left\{
\begin{array}{l}
\mathrm{rot}(\bm{X}\times\bm{Y})=(\bm{Y}\cdot\nabla)\bm{X}-(\bm{X}\cdot\nabla)\bm{Y}+\bm{X}\mathrm{div}\bm{Y}-\bm{Y}\mathrm{div}\bm{X}\\
\\
\mathrm{div}\displaystyle\frac{\bm{r}}{r^3}=-\mathrm{divgrad}\frac{1}{r}=4\pi\delta(\bm{r})\\
~
\end{array}
\right.}\nonumber
\end{eqnarray}

参考文献

[1] 中村徹『電磁気学　第2版』、日本評論社、2017
[2] David J. Griffiths『Introduction to Electrodynamics』, Pearson Education, 2013