$\def\bm#1{{\boldsymbol{#1}}}$
$\def\rmd#1{\mathrm{d}{#1}}$
$\def\Braket#1{\langle{#1}\rangle}$
$\def\Bra#1{\langle{#1}|}$
$\def\Ket#1{|{#1}\rangle}$
$\def\kb{k_{\text{B}}}$
$\def\dag{\dagger}$
$\def\rmd{\mathrm{d}}$

古典力学03

剛体の力学

大学の試験では時間の制約上、複雑な系のオイラーの運動方程式を解くという問題が出題されることはあまりない。従って、出題される計算問題は質量と重心、トルクのつり合い、慣性モーメント、角運動量保存則、実体振り子の周期など簡単に解ける運動、剛体の解析力学、のせいぜい$6$パターンほどである。剛体の解析力学は後で触れる。

質量と重心

質量は密度関数を$\rho$として、以下で定義される。
\begin{equation}
M=\int\rho~\rmd V
\end{equation}
重心は以下の定義から計算できる
\begin{equation}
\bm{r}_\mathrm{G}=\dfrac{\int\bm{r}\rmd m}{M},~\bm{r}_\mathrm{G}=\dfrac{\sum_i\bm{r}_im_i}{M}
\end{equation}
である。これらの計算パターンの多くは$1$次元の棒などの積分であるが、稀に重積分を実行しなければならない場合もある。その場合は、ヤコビアンを忘れないこと。

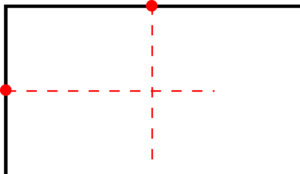
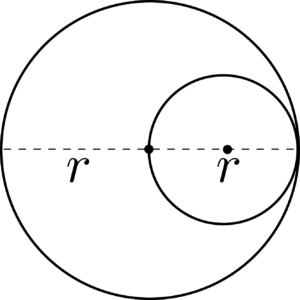
一方で、積分をしなくとも算数的に重心を求めることができる例もある。「考えている物体を分けたときのそれぞれの重心が元々の物体の重心となる。」という方針で解いていく。典型的には、図のようなカギ括弧形と円をくりぬいた形が頻出である。円をくりぬかれている場合は円があった場合を考えて、求める重心と埋め込んだ円の重心が大きな円の重心になるというプロセスで解けばよい。

トルクのつり合い

$1$つの質点の位置は座標$(x,y,z)$の$3$つの値を指定すると決まる。これに対して、剛体では重心の座標$(x_\mathrm{G},y_\mathrm{G},z_\mathrm{G})$と各座標軸まわりの回転角度$3$つを併せた$6$つの値を指定する必要がある。

$1$個の剛体に複数の力$\bm{F}_i$がそれぞれ$\bm{r}_i$の位置に働いているが力はつり合っており剛体は静止しているとする。このとき、力のつり合いより$\sum_i\bm{F}_i=\bm{0}$、剛体が回転していないことから$\sum_i\bm{r}_i\times\bm{F}_i=\bm{0}$が成り立つ。これらを併せると$6$本の式が成り立っているため、$6$自由度の値が一意的に決定できることになる。

慣性モーメント

剛体が少数の粒子で作られている場合、与えられた回転軸のまわりの慣性モーメントは$T=\sum_im_ir_i^2$で計算できる。剛体が無数の粒子からなる場合、物体の慣性モーメントは以下の式で定義される。
\begin{equation}
I=\int r^2\rmd m=\int \rho r^2\rmd V
\end{equation}
この式によって任意の軸まわりの慣性モーメントをいつでも求めることができる。しかし、その軸に平行で物体の重心を通る軸まわりの慣性モーメント$I_{\mathrm{G}}$が既に分かっている場合は平行軸の定理が便利である。平行軸の定理によれば、質量$M$の物体の重心から$R$だけ離れた軸まわりの慣性モーメント$I$は、その軸に平行で物体の重心を通る軸まわりの慣性モーメント$I_{\mathrm{G}}$を用いて次のようにあらわすことができる。
\begin{equation}
I=I_\mathrm{G}+MR^2
\end{equation}
教科書では試験冊子の表紙で、細い棒の慣性モーメント$I=(Ml^2)/12$、薄い円盤の慣性モーメント$I=(MR^2)/2$、球体の慣性モーメント$I=(2MR^2)/5$という公式がそれぞれ与えられているため、これらに関して記憶しておく必要はない。

剛体における運動エネルギーと角運動量の保存則

転がる剛体の運動エネルギーは重心の並進運動に関する運動エネルギーと重心まわりの回転運動に関する運動エネルギーの和であらわされる。これは次のように書くことができる。
\begin{equation}
\dfrac{1}{2}m_\mathrm{i}v_\mathrm{i}^2+\dfrac{1}{2}I_\mathrm{i}\omega_\mathrm{i}^2=\dfrac{1}{2}m_\mathrm{f}v_\mathrm{f}^2+\dfrac{1}{2}I_\mathrm{f}\omega_\mathrm{f}^2
\end{equation}
この式を用いて角速度などを計算させる問題が頻出であるが、このときの慣性モーメントは前述の平行軸の定理を利用する場合が多い。

一方、考えている剛体に外部から働く正味のトルクがゼロのとき、剛体の角運動量は保存する。これは次のように書くことができる。
\begin{equation}
I_\mathrm{i}\omega_\mathrm{i}=I_\mathrm{f}\omega_\mathrm{f}
\end{equation}
この角運動量保存則が有効的に成り立っている例としてはフィギュアスケートの回転などがある。