$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\rmd}{\mathrm{d}}$

第04講の導入

第02講で1次元空間内の運動学を考えました。第04講では、第03講でやった数学的準備をもとにして、これを2、3次元に拡張することを考えていきます。1次元空間内では座標系は1通りしかありませんでしたが、2、3次元の場合はデカルト座標（$x$、$y$、$z$で表す座標系）以外の座標系を用いた方が計算しやすいことがあります。前半は他の座標系について紹介しながら2、3次元空間内の運動学を考えていきましょう。後半は運動の軌跡の接線、法線、曲率半径を導入します、これはベクトル解析を理解する助けになればと思います。

2・3次元空間内の位置、速度、加速度

第02講の議論を拡張すれば、時刻$t$に位置$\bm{r}(t)$にあった物体が時刻$t+\Delta t$に$\bm{r}(t+\Delta t)$に移動したときの変位を表すと以下のようになります。
\[
\bm{r}(t+\Delta t)-\bm{r}(t)
\]
第03講での復習になりますが、ここでの$\bm{r}(t)$は高校数学のベクトルでやった位置ベクトルを指します。ベクトルは高校では$\vec{r}$または$\overrightarrow{\mathrm{OR}}$などとしていましたが、大学では太字にして$\bm{r}$と表します。ただ単に表記が変わっただけですから混乱しないようにしてください。

さて、同様にして速度$\bm{v}(t)$と加速度$\bm{a}(t)$も以下のように定義します。
\[
\bm{v}(t)\coloneqq\lim_{\Delta t\rightarrow0}\frac{\bm{r}(t+\Delta t)-\bm{r}(t)}{\Delta t}
\]
\[
\bm{a}(t)\coloneqq\lim_{\Delta t\rightarrow0}\frac{\bm{v}(t+\Delta t)-\bm{v}(t)}{\Delta t}
\]
今、$\bm{r}=(x(t)、y(t)、z(t))$なので、$x$、$y$、$z$軸方向の単位ベクトルをそれぞれ$\bm{i}$、$\bm{j}$、$\bm{k}$と表すと$\bm{r}(t)=x\bm{i}+y\bm{j}+z\bm{k}$と書けることになりますから、これを速度と加速度の式に代入すれば、以下のように速度と加速度をそれぞれ成分ごとに分解することが出来ます。
\[
\bm{v}(t)=\frac{dx(t)}{dt}\bm{i}+\frac{dy(t)}{dt}\bm{j}+\frac{dz(t)}{dt}\bm{k}
\]
\[
\bm{a}(t)=\frac{d^2x(t)}{dt^2}\bm{i}+\frac{d^2y(t)}{dt^2}\bm{j}+\frac{d^2z(t)}{dt^2}\bm{k}
\]
すなわち、デカルト座標系における位置、速度、加速度の関係は軸方向の成分に分解されるため、1次元における定義を自然に拡張することで成立します。

2次元座標系

2次元空間にはデカルト座標$(x、y)$の他によく使う座標系として2次元極座標$(r、\theta)$があります。図4.1よりデカルト座標$(x、y)$と2次元極座標$(r、\theta)$の間には関係式があります。$x$、$y$をそれぞれ$r$、$\theta$で表すときは$x=r\cos\theta$、$y=r\sin\theta$と書けます。一方、$r$、$\theta$をそれぞれ$x$、$y$で表すときはピタゴラスの定理から分かる$r=\sqrt{x^2+y^2}$と$\tan\theta=y/x$と書けます。大学の微分積分でやる$\tan A$の逆関数、$\arctan A$を利用すれば$\theta=\arctan(y/x)$と書けます。両者の関係式は今後頻繁に使用しますから、今のうちに慣れておいてください。

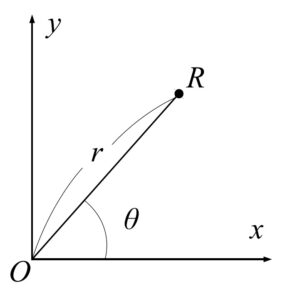
図4.1　2次元極座標

3次元座標系

3次元空間にはデカルト座標$(x、y、z)$の他によく使う座標系として3次元極座標$(r、\theta、\varphi)$と円柱座標$(r、\varphi、z)$があります。まず3次元極座標から説明します。デカルト座標と3次元極座標の間の関係式は2次元極座標と同様に考えると以下のようになります。
\[
\left\{
\begin{array}{l}
x=r\sin\theta\cos\varphi\\
\\
y=r\sin\theta\sin\varphi\\
\\
z=r\cos\theta
\end{array}
\right.　\mathrm{and}
\left\{
\begin{array}{l}
r=\sqrt{x^2+y^2+z^2}\\
\\
\theta=\arctan\left(\displaystyle\frac{\sqrt{x^2+y^2}}{z}\right)\\
\\
\varphi=\arctan\left(\displaystyle\frac{y}{x}\right)
\end{array}
\right.
\]

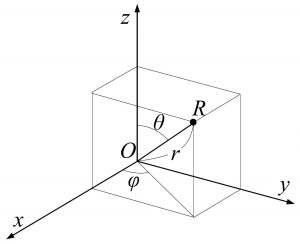
図4.2　3次元極座標

次に円柱座標について説明します、円柱座標は2次元極座標と$z$との組み合わせで作られた座標で、螺旋運動を表すときなどに使用します。デカルト座標と円柱座標の間の関係式は以下のようになります。
\[
\left\{
\begin{array}{l}
x=\rho\cos\varphi\\
\\
y=\rho\sin\varphi\\
\\
z=z
\end{array}
\right.　\mathrm{and}
\left\{
\begin{array}{l}
\rho=\sqrt{x^2+y^2}\\
\\
\theta=\arctan\left(\displaystyle\frac{y}{x}\right)\\
\\
z=z
\end{array}
\right.
\]

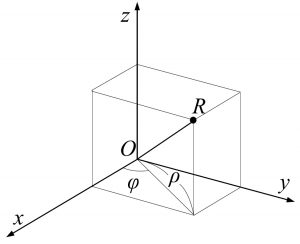
図4.3　円柱座標

2次元極座標の速度、加速度

具体的な計算練習として2次元極座標の速度と加速度を計算してみましょう。動径方向（原点からある点に向かう方向）の単位ベクトルとそれに直交する原点の周りを反時計回り方向に向く単位ベクトルをそれぞれ$\bm{e}_r$と$\bm{e}_\theta$としておきます。

まず、$\bm{r}$は2次元極座標で$\bm{r}=r\bm{e}_r$と記述することが出来ます。これを用いると速度$\bm{v}$は以下のように書けます。
\[
\bm{v}(t)=\frac{dr}{dt}\bm{e}_r+r\frac{d\bm{e}_r}{dt}
\]
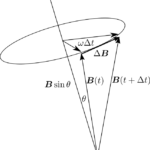
右辺第1項は動径方向の腕の長さが変わる効果を表しており、右辺第2項は腕が回転する効果を表していることが分かります。図4.4より$|\bm{e}_r(t+\Delta t)-\bm{e}_r(t)|\simeq|\theta(t+\Delta t)-\theta(t)|$が成り立っているので動径ベクトルの速度は以下のように書けます。
\[
\frac{d\bm{e}_r(t)}{dt}\coloneqq\lim_{\Delta\rightarrow0}\frac{\bm{e}_r(t+\Delta t)-\bm{e}_r(t)}{\Delta t}=\lim_{\Delta\rightarrow0}\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\bm{e}_\theta(t)=\dot{\theta}\bm{e}_\theta
\]

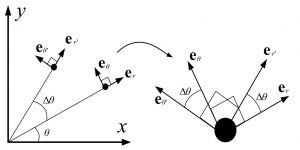
図4.4　2次元極座標の単位ベクトルの動き

これらより速度$\bm{v}$について以下の関係式が導かれます。
\[
\bm{v}(t)=\dot{r}\bm{e}_r+r\dot{\theta}\bm{e}_\theta
\]
同様に加速度も計算をしてみましょう。無限に短い時間の間に$\bm{e}_\theta$が動く方向は自身に垂直かつ$\bm{e}_r$の逆方向になるということから分かる$\dot{\bm{e}_\theta}(t)=-\dot{\theta}\bm{e}_r$という関係を利用します。加速度$\bm{a}$には以下の関係式が成り立ちます。
\[
\bm{a}(t)=\frac{d}{dt}(\dot{r}\bm{e}_r+r\dot{\theta}\bm{e}_\theta)=\ddot{r}\bm{e}_r+\dot{r}\dot{\bm{e}}_r+\dot{r}\dot{\theta}\bm{e}_\theta+r\dot{\theta}\bm{e}_\theta+r\ddot{\theta}\bm{e}_\theta+r\dot{\theta}\dot{\bm{e}_\theta}
\]
これらより加速度$\bm{a}$について以下の関係式が導かれます。
\[
\bm{a}(t)=(\ddot{r}-r\dot{\theta}^2)\bm{e}_r+(r\ddot{\theta}+2\dot{r}\dot{\theta}\bm{e}_\theta)
\]
特に等速円運動の場合を考えてみましょう。半径を$R（一定）$、角速度$\dot{\theta}=\omega（一定）$とすると$\ddot{\theta}=\dot{r}=0$となるから、以下の式が導けます。
\[
\left\{
\begin{array}{l}
v_r\coloneqq\dot{r}=0\\
\\
v_\theta\coloneqq r\dot{\theta}=R\omega\\
\\
a_r\coloneqq\ddot{r}-r\dot{\theta}^2=-R\omega^2\\
\\
a_\theta\coloneqq r\ddot{\theta}+2\dot{r}\dot{\theta}=0
\end{array}
\right.
\]
従って、等速円運動の場合、接線方向への速度と中心方向への加速度、すなわち向心加速度を受けていることが分かりました。

運動の軌跡の接線、法線、曲率半径

次に質点の運動の軌跡を特徴づけるために接線、法線、曲率半径の考え方を導入します。質点の位置ベクトル$\bm{r}(t)$と速度$\bm{v}(t)=\dot{\bm{r}}(t)$について、その瞬間の運動方向を表す単位ベクトルのことを接線ベクトルと呼びます。接線ベクトル$\bm{e}_\mathrm{t}$は以下のように定義されます。
\[
\bm{e}_\mathrm{t}\coloneqq\frac{\bm{v}}{|\bm{v}|}
\]
ここで、下付き添え字のt はtangential を意味します。さて、軌跡に接する円を描くことを考えてみましょう。軌跡に円が接するためには、円が軌道の接線$\bm{e}_\mathrm{t}(t)$に接し、微小時間$\Delta t$で$|\bm{v}(t)|\Delta t$だけ移動した後の接線$\bm{e}_\mathrm{t}(t+\Delta t)$にも接している必要があります。$|\bm{v}(t)|\Delta t$だけ進んだときに$|\bm{e}_\mathrm{t}(t+\Delta t)-\bm{e}_\mathrm{t}(t)|$だけ回転するために、接線の半径を$\rho$とすると、相似の関係から以下の関係式が導けます。
\[
\frac{|\bm{v}(t)|\Delta t}{\rho}\simeq\frac{|\bm{e}_\mathrm{t}(t+\Delta t)-\bm{e}_\mathrm{t}(t)|}{1}
\]
これは当然$|\bm{e}_\mathrm{t}(t+\Delta t)-\bm{e}_\mathrm{t}(t)|\rightarrow0$のときに厳密に成り立ちます。$1/\rho$のことを曲率、$\rho$のことを曲率半径と呼びます。従って、曲率半径は以下の式になると分かります。
\[
\rho=\lim_{|\bm{e}_\mathrm{t}(t+\Delta t)-\bm{e}_\mathrm{t}(t)|\rightarrow0}\frac{|\bm{v}(t)|\Delta t}{|\bm{e}_\mathrm{t}(t+\Delta t)-\bm{e}_\mathrm{t}(t)|}=\lim_{\Delta t\rightarrow0}\frac{\left\{\displaystyle\frac{|\bm{v}(t)|\Delta t}{\Delta t}\right\}}{\left\{\displaystyle\frac{|\bm{e}_\mathrm{t}(t+\Delta t)-\bm{e}_\mathrm{t}(t)|}{\Delta t}\right\}}=\frac{|\bm{v}|}{|\dot{\bm{e}}_\mathrm{t}|}
\]
さて、次に$|\dot{\bm{e}}_\mathrm{t}|$を計算しましょう。これは以下のように計算できます。
\[
|\dot{\bm{e}}_\mathrm{t}|=\left|\frac{\bm{a}}{|\bm{v}|}-\frac{\bm{v}}{|\bm{v}|^2}\frac{d|\bm{v}|}{dt}\right|=\frac{1}{|\bm{v}|^2}\sqrt{|\bm{v}|^2|\bm{a}|^2-(a_xv_x+a_yv_y)^2}
\]
これを曲率半径の式に代入すると、以下のようになります。
\[
\rho=\frac{|\bm{v}|^3}{\sqrt{|\bm{v}|^2|\bm{a}|^2-(a_xv_x+a_yv_y)^2}}
\]
但し、ここまでの議論において、速度の大きさの微分$d|\bm{v}|/dt$と速度の微分の大きさ$|d\bm{v}/dt|$を混同しないように十分注意してください。これらの量は一般には一致しません。例えば、先程の等速円運動の例だと$d|\bm{v}|/dt=0$ですが$|d\bm{v}/dt|＝R\omega^2$となります。

サイクロイド運動の解析

ここまでの話を具体的な計算で確認してみましょう。サイクロイド曲線、
\[
\left\{
\begin{array}{l}
x=R(\omega t-\sin\omega t)\\
y=R(1-\cos\omega t)
\end{array}
\right.
\]
を考えます。速度ベクトル$\bm{v}$は以下のように計算できます。
\[
\bm{v}=\frac{d\bm{r}}{dt}=(R\omega-R\omega\cos\omega t、R\omega\sin\omega t)
\]
これを用いると速さは以下のようになります。
\[
|\bm{v}|=R\omega\sqrt{(1-\cos\omega t)^2+\sin^2\omega t}=2R\omega\left|\sin\frac{\omega t}{2}\right|
\]
加速度ベクトル、加速度の大きさはそれぞれ以下のように計算できます。
\[
\bm{a}=\frac{d\bm{v}}{dt}=(R\omega^2\sin\omega t、R\omega^2\cos\omega t)
\]
\[
|\bm{a}|=R\omega^2
\]
よってサイクロイドの曲率半径はこれらを代入して以下のように求まります。
\[
\rho=4R\sin\left|\frac{\omega t}{2}\right|
\]
これによってサイクロイドの曲率半径は時間によって周期的に変動することが分かりました。

第04講のまとめ

最後に一言コメントをして第04講を終わりにしましょう。第02講と第04講で運動学の初歩を学びました。ここまでの4回の講義で、微分積分やベクトル解析などの物理数学が物理で重要な役割を持っていそうだということは感じてもらえたと思います。この後はここまででやった内容をもとにして、運動が起こる原因を問うていくという形になっていきます。数学的な計算に溺れないようにしっかりと紙とペンを用意して自ら計算を追って行ってください。