$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\rmd}{\mathrm{d}}$

振動する弦のモデル化

イントロダクション

物理学・工学において重要な偏微分方程式の1つに波動方程式と呼ばれる$2$階偏微分方程式があります。

ここでは1次元の場合に話を限定して波動方程式の基礎事項について論じることにします。波動方程式は様々な物理現象において顔を出す方程式です。

例えば、バイオリンの弦のような弾性的な弦の微小横振動の波を記述する方程式はこの波動方程式です。後で見ていくように、高校物理の波動論の分野で丸暗記していた式のいくつかはこの波動方程式及びその解から得られる帰結に過ぎないことが分かります。また、これまでに物理で出てきたPoisson 方程式（Laplace 方程式）や熱拡散方程式は変数分離法が主要な解法でしたが、$1$次元の波動方程式には変数分離法に加えてd’ Alembert の解法と呼ばれる非常に特徴的な解法が存在します（2次元以上の波動方程式は解の求積に高度な特殊関数論の知識と膨大な計算が要求されるため、ここでは論じないことにします。）。

d’ Alembert の解法の主張は数式で見ると掴みづらいですが、図を描いてみれば意外と簡単なことを言っているに過ぎないのです。これらのことを以下の全3回の講座で具体的に手を動かしながら確認していきましょう。

まず今回は一番直感的かつ簡単な例である弦の振動を例にして波動方程式を導出します。古典力学としてのスケールで見て本質的な部分にのみ焦点を当てた「良い近似」によって導出される方程式が波動方程式なのだということを実感することが目標です。次の回ではこれまでの偏微分方程式と同様の解法である変数分離法を用いた解析を行います。ここではFourier 解析の計算を思い出しながら計算を追ってほしいと思います。そして第3講ではd’ Alembert の解法による解の求積を議論します。ここでは、d’ Alembert の解法の主張が非常に直感的なものであることを理解したいです。

振動する弦のモデル化

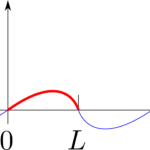
下図のように弦を$x$軸に沿って張り、長さが$L$になるように伸ばし、弦の両端を$x=0,L$で固定します。弦を適当な形に変形させて、$t=0$で振動を開始させて$t>0$での弦の形を求めるという問題を考えます。すなわち、任意の位置$x$と任意の時刻$t$での弦の変位$u(x、t)$を求めたいです。

図1　ある時刻$t$において振動する弦

ここでは、以下のような物理的仮定（近似）をおくことになります。

• (1)弦はいたるところで均質であるとする。すなわち、弦の単位長さ当たりの質量は一定であり、弦は完全に弾性的で曲げに対する抵抗がないとする。
• (2)弦を両端で固定するときに弦を伸ばすが、その時の張力は弦に働く重力に比べて十分大きいとする。すなわち、重力の影響は無視する。
• (3)弦は垂直面内で微小な横運動を行うとする。すなわち、弦の各点は厳密に垂直方向のみに動き、各点における弦の変位と傾きの絶対値は小さいとする。

これらの仮定から得られる偏微分方程式の解$u(x、t)$は実際の運動の最も本質的な部分を上手く記述すると期待できるでしょう。

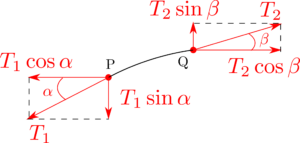
図2　弦の張力の成分分解

微分方程式を導くため、弦の微小部分に働く力を考えましょう（図1, 2）。仮定(2)より、弦は曲げに対して抵抗がないので、弦の各点で接線方向に張力が働くと考えてよいことになります。微小部分の端点P とQ での張力をそれぞれ$T_1$と$T_2$としましょう。弦の各点は垂直方向に動き、水平方向には運動しないです。従って、張力の水平成分は一定でなければなりません。図1の記号を用いると

$$\begin{equation} T_1\cos{\alpha}=T_2\cos{\beta}=T=\text{Const.}\tag{1} \end{equation}$$

であることになります。垂直方向には$-T_1\sin{\alpha}$と$T_2\sin{\beta}$の$2$つの方向が働きます。変形していない弦の単位長さ当たりの質量と弦の微小部分の長さをそれぞれ$\rho$と$\Delta x$とすると、微小部分PQの質量は$\rho\Delta x$です。また、$x$と$x+\Delta x$の間の点で測った加速度は$\partial^2u/\partial t^2$なので、運動方程式は以下のように書けます。

$$\begin{equation} \rho\Delta x\dfrac{\partial^2u}{\partial t^2}=T_2\sin{\beta}-T_1\sin{\alpha}\tag{2} \end{equation}$$

式(2)の右辺第$1$項を式(1)の$T_2\cos{\beta}$で割り、右辺第$2$項を式(1)の$T_1\cos{\alpha}$で割り、左辺を$T$で割ると、以下の式を得ることができます。

$$\begin{equation} \dfrac{T_2\sin{\beta}}{T_2\cos{\beta}}-\dfrac{T_1\sin{\alpha}}{T_1\cos{\alpha}}=\tan{\beta}-\tan{\alpha}=\dfrac{\rho\Delta x}{T}\dfrac{\partial^2u}{\partial t^2}\tag{3} \end{equation}$$

$\tan{\alpha}$と$\tan{\beta}$はそれぞれ$x$と$x+\Delta x$での弦の曲線の傾きであるから、以下のようにあらわすこともできます。

$$\begin{equation} \tan{\alpha}=\left(\dfrac{\partial u}{\partial x}\right)\biggr|_{x}、~~~\tan{\beta}=\left(\dfrac{\partial u}{\partial x}\right)\biggr|_{x+\Delta x}\tag{4} \end{equation}$$

$u$は$t$にも依存する関数なので、偏微分で傾きをあらわしていることに注意が必要です。さて、式(3)を$\Delta x$で割ると、

$$\begin{equation} \dfrac{1}{\Delta x}\left[\left(\dfrac{\partial u}{\partial x}\right)\biggr|_{x+\Delta}-\left(\dfrac{\partial u}{\partial x}\right)\biggr|_{x}\right]=\dfrac{\rho}{T}\dfrac{\partial^2u}{\partial t^2}\tag{5} \end{equation}$$

となります。この式に対して$\Delta x\rightarrow0$の極限を取ると、次の$2$階線型偏微分方程式を得ることができます。

もしここの式変形に納得できなければ、$\partial u/\partial x=F(x、t)$とおいてみると良いです。そうすると式(5)の左辺に対して$\Delta x\rightarrow0$の極限を取るという操作は
$$\lim_{\Delta x\rightarrow0}\dfrac{F(x+\Delta x、t)-F(x、t)}{\Delta x}=\dfrac{\partial}{\partial x}F(x、t)=\dfrac{\partial^2u}{\partial x^2}$$
と書けることが分かるでしょう。

$$\begin{equation} \dfrac{1}{v^2}\dfrac{\partial^2u}{\partial t^2}=\dfrac{\partial^2u}{\partial x^2}~~~\text{where}~v=\sqrt{\dfrac{T}{\rho}}>0\tag{6} \end{equation}$$

これがこの問題を記述する方程式であり、1次元波動方程式と呼ばれています。物理定数$T/\rho$を$v$ではなく$v$の2乗と定義しましたが、これは$T/\rho$が正の量であることを示すためです。これは「弦を伝わる波の速さの公式」として高校物理で習った関係式であることを思い出しておきましょう。

なお、「1次元」というのは方程式にあらわれている空間座標が$x$のみであることをあらわしています。同様にして、例えば、

$$\begin{equation} \dfrac{1}{v^2}\dfrac{\partial^2u}{\partial t^2}=\dfrac{\partial^2u}{\partial x^2}+\dfrac{\partial^2u}{\partial y^2}\tag{7} \end{equation}$$

であれば2次元の波動方程式と呼びます。今は1次元の波動方程式を導出するために弦の振動を考えていましたが、2次元の波動方程式を導出するためには膜の振動を考える必要があります。