$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\rmd}{\mathrm{d}}$

変数分離法による解の求積

前回、弾性弦の振動が以下の1次元波動方程式で記述されるということを示しました。

$$\begin{equation} \dfrac{1}{v^2}\dfrac{\partial^2u}{\partial t^2}=\dfrac{\partial^2u}{\partial x^2}~~~\text{where}~v=\sqrt{\dfrac{T}{\rho}}>0\tag{8} \end{equation}$$

但し、$u(x,t)$は弦の変位です。弦がどのように運動するかを調べるためにはこの方程式を解かなければなりません。厳密にいうと、(8)を満たす$u(x,t)$の中で物理系に課せられている条件を満たしているものが適切な解です。これらの条件について以下で考えることにしましょう。

まず、端点$x=0$と$x=L$で弦が固定されているので、$2$つの境界条件

$$\begin{equation} u(0、t)=0、~~~u(L、t)=0~~~~~\text{for all }t\tag{9} \end{equation}$$

が得られます。加えて、初期変位（$t=0$での変位）と初速度（$t=0$での速度）によって弦の運動の様子が変わるということです。初期変位を$f(x)$、初速度を$g(x)$とすると、

$$\begin{equation} u(x、0)=f(x)、~~~\dfrac{\partial u}{\partial t}\biggr|_{t=0}=g(x)\tag{10} \end{equation}$$

が得られる。式(10)を初期条件と言います。従って、問題は、式(8)のうち境界条件(9)と初期条件(10)を満たすものを求めるということです。この求積をここでは以下の手順で行います。

• ステップ1：変数分離法を利用して、考えている偏微分方程式を$2$つの常微分方程式の問題に直す。
• ステップ2：得られた$2$つの常微分方程式の解で、かつ境界条件(9)を満たすものを求める。
• ステップ3：求めた解を組み合わせて、波動方程式(8)の解であり、かつ初期条件(10)を満たすものを見つける。

ステップ1：2つの常微分方程式を得ること

変数分離法では、方程式(8)の解を

$$\begin{equation} u(x,t)=X(x)T(t)\tag{11} \end{equation}$$

という形であると仮定して話を進めます。これは$2$つの関数の積で、それぞれの関数は変数$x$と$t$のみにそれぞれ依存しています。この式を$x$と$t$で$2$回ずつ微分すると、

$$\begin{equation} \dfrac{\partial^2u}{\partial t^2}=X\ddot{T}、~~~\dfrac{\partial^2u}{\partial x^2}=X”T(t)\tag{12} \end{equation}$$

となります。但し、ドット$\dot{}$は$t$に関する微分をあらわし、プライム$’$は$x$に関する微分をあらわすものとします。これを式(8)に代入すると、以下の式を得ます。

$$\begin{equation} X\ddot{T}=v^2X”T\tag{13} \end{equation}$$

この式の両辺を$v^2X,T\neq0$で割ると、

$$\begin{equation} \dfrac{\ddot{T}}{v^2T}=\dfrac{X”}{X}\tag{14} \end{equation}$$

を得ます。上式の両辺は定数でなければなりません。左辺は$t$のみの関数で、右辺は$x$のみの関数なので、それらが等しいということは定数以外ありえないためです。このことから、ある定数$k$を用いて

$$\begin{equation} \dfrac{\ddot{T}}{v^2T}=\dfrac{X”}{X}=k\tag{15} \end{equation}$$

と書くことができます。$A=B=C$という式は$A=C$と$B=C$という$2$つの方程式に分解できるので、これから直ちに$2$つの常微分方程式

$$X”-kX=0\tag{16a}$$
$$\ddot{T}-v^2kT=0\tag{16b}$$

を得ます。今のところ$k$は任意の定数となっていますが、境界条件を考慮すると$k$には制限が課されます。これについて次のステップで考えることにしましょう。

ステップ2：境界条件を満足すること

式(16a)と式(16b)から$X(x)$と$T(t)$を決めて、$u=X,T$が境界条件(9)を満たすようにします。すなわち、

$$u(0,t)=X(0)T(t)=0\tag{17a}$$
$$u(L,t)=X(L)T(t)=0\tag{17b}$$

について考えることになります。

まず、(16a)の解について考えましょう。式(11)で$T(t)=0$ならば、明らかに$u=0$となり、これは意味のない解です。従って、$T\neq0$とすると、

$$X(0)=0\tag{18a}$$
$$X(L)=0\tag{18b}$$
となります。

$k=0$のときは、式(16a)の一般解は$X(x)=ax+b$となり、式(18a,18b)から$a=b=0$、すなわち、$X(x)=0$が得られるので$u=0$となります。これも意味のない解です。次に、$k>0$として$k=\mu^2$とおくと、式(16a)の一般解は$X(x)=a\mathrm{e}^{\mu x}+b\mathrm{e}^{-\mu x}$となり、先ほどと同様に式(18a,18b)から$a=b=0$、すなわち、$X(x)=0$が得られるので$u=0$となります。これも意味のない解である。

従って、意味のある解を得るための残る可能性は$k<0$として$k=-p^2$とおくことのみとなります。このときの一般解は

$$\begin{equation} X(x)=a\cos{(px)}+b\sin{(px)}\tag{19} \end{equation}$$

です。これと式(18a,18b)から$a=0$、更に$b\sin{(pL)}=0$を得ます。$b=0$とすると$X(x)=0$となって意味のない解となってしまうので、$b\neq0$とおかなければなりません。従って、$\sin{(pL)}=0$であるから、

$$\begin{equation} pL=n\pi~~~\text{i.e.,}~~~p=\dfrac{n\pi}{L}~、~n\in\mathbb{Z}\tag{20} \end{equation}$$

となります。$b=1$とおくと無限に多くの解

$$\begin{equation} X(x)=X_n(x)=\sin{\left(\dfrac{n\pi x}{L}\right)}~、~n\in\mathbb{N}\tag{21} \end{equation}$$

が得られます。この解は式(18a,18b)を満たします。$\sin{(-\alpha)}=-\sin{\alpha}$であることから$n$が負の整数のときには符号が変わるだけで同じ形の解が得られると解釈して、$n$の範囲が任意の整数から任意の自然数に変わっていることに注意が必要です。

このように$k$が限定されて、式(20)から$k=-p^2=-(n\pi/L)^2$となります。この$k$の値に対して、方程式(16b)は

$$\begin{equation} \ddot{T}+\lambda_n^2T=0~~~\text{where}~~~\lambda_n=\dfrac{vn\pi}{L}\tag{22} \end{equation}$$

という形になります。一般解は

$$\begin{equation} T_n(t)=A_n\cos{(\lambda_nt)}+B_n\sin{(\lambda_nt)}\tag{23} \end{equation}$$

です。従って、関数$u_n(x,t)=X_n(x)T_n(t)$は、

$$\begin{equation} u_n(x,t)=\biggl\{A_n\cos{(\lambda_nt)}+B_n\sin{(\lambda_nt)}\biggr\}\sin{\left(\dfrac{n\pi x}{L}\right)}~、~n=1、2、\ldots\tag{24} \end{equation}$$

と書けます。

固有関数について

$u_n(x,t)$は式(9)を満たす式(8)の解です。関数$u_n$を振動弦の固有関数と呼び、$\lambda_n$を固有値と呼びます。また、このときの集合$\{\lambda_1、\lambda_2、\cdots、\lambda_n\}$のことをスペクトルと呼びます（これらの用語が線型代数における用語と同じものであることに気が付いた人がいるかもしれません。実は直交関数論を学ぶと、関数とベクトルは殆ど同じものであるということが明らかとなります。）。

今考えている波の周期は$2\pi$なので、（振動数）$=$（波長）$/$（周期）であることを思い出すと、それぞれの$u_n$は、振動数が$f_n=\lambda_n/(2\pi)=vn/(2L)$である調和振動をあらわします。この運動の弦を第$n$標準モードと呼びます。第$1$標準モードは基本モード（$n=1$）、その他の標準モードは上音として知られています。音楽用語でいうと、それらはオクターブ、オクターブ$+5$度などを与えるものです。式(24)で

$$\begin{equation} \text{For}~x=\dfrac{L}{n}、\dfrac{2L}{n}、\cdots、\dfrac{(n-1)L}{n}、~~~\sin{\left(\dfrac{n\pi x}{L}\right)}=0\tag{25} \end{equation}$$

であるので、一般に第$n$標準モードは$n-1$個の節を有します。ここで、節とは弦の動かない点（但し、端点は除く）のことです。

ステップ3：問題の一般解を得ること

単一の解$u_n(x,t)$では、一般に初期条件(10)を満たすことができません。ところで、方程式(8)は線型かつ同次の方程式であるので、有限個の$u_n$の重ね合わせも方程式(8)の解であることが言えます。初期条件(10)を満たす解を得るため、無限級数

$$\begin{equation} u(x,t)=\sum_{n=1}^\infty u_n(x,t)=\sum_{n=1}^\infty\biggl\{A_n\cos{(\lambda_nt)}+B_n\sin{(\lambda_nt)}\biggr\}\sin{\left(\dfrac{n\pi x}{L}\right)}\tag{26} \end{equation}$$

を考えましょう（前と同じく、$\lambda_n=vn\pi/L$であるとします。）。

式(26)と初期条件から、

$$\begin{equation} u(x、0)=\sum_{n=1}^\infty A_n\sin{\left(\dfrac{n\pi x}{L}\right)}=f(x)\tag{27} \end{equation}$$

となります。従って、$u(x、0)$が$f(x)$のFourier 正弦級数になるように係数$A_n$を選ばなければなりません。故に、

$$\begin{equation} A_n=\dfrac{2}{L}\int_0^Lf(x)\sin{\left(\dfrac{n\pi x}{L}\right)}dx\tag{28} \end{equation}$$

です。$f(x)$は初期変位に対応しています。同様に(26)を$t$で微分して初期条件を用いると、

$$\begin{align} \dfrac{\partial u}{\partial t}\biggr|_{t=0}=&\left[\sum_{n=1}^\infty\biggl\{-A_n\lambda_n\sin{(\lambda_nt)}+B_n\lambda_n\cos{(\lambda_nt)}\biggr\}\sin{\left(\dfrac{n\pi x}{L}\right)}\right]_{t=0}\nonumber =&\sum_{n=1}^\infty B_n\lambda_n\sin{\left(\dfrac{n\pi x}{L}\right)}=g(x)\tag{29} \end{align}$$

となります。$g(x)$は初速度に対応している。従って、最後の等号が成立するようにFourier 係数$B_n$を選べば良いことになります。すなわち、

$$\begin{equation} B_n\lambda_n=\dfrac{2}{L}\int_0^Lg(x)\sin{\left(\dfrac{n\pi x}{L}\right)}dx\tag{30} \end{equation}$$

です。$\lambda_n=vn\pi/L$であるので、上式は以下のように書けます。

$$\begin{equation} B_n=\dfrac{2}{vn\pi}\int_0^Lg(x)\sin{\left(\dfrac{n\pi x}{L}\right)}dx\tag{31} \end{equation}$$

このように、式(26)の解は最初は単に形式的なものでした。ここでは式(26)が妥当なものであることを示しましょう。議論を簡単にするために、初速度が$0$、すなわち$g(x)=0$の場合を考えることにします。この場合、$B_n=0$なので式(26)は

$$\begin{equation} u(x,t)=\sum_{n=1}^\infty A_n\cos{(\lambda_nt)}\sin{\left(\dfrac{n\pi x}{L}\right)}~~~\text{where}~\lambda_n=\dfrac{vn\pi}{L}\tag{32} \end{equation}$$

となります。この級数の和は三角関数の積和公式

$$\begin{equation} \cos{\alpha}\sin{\beta}=\dfrac{1}{2}\biggl\{\sin{(\beta-\alpha)}+\sin{(\beta+\alpha)}\biggr\}\tag{33} \end{equation}$$

を用いて以下のように書き直すことができます。

$$\begin{equation} u(x,t)=\dfrac{1}{2}\sum_{n=1}^\infty B_n\sin\left\{\dfrac{n\pi}{L}(x-vt)\right\}+\dfrac{1}{2}\sum_{n=1}^\infty B_n\sin\left\{\dfrac{n\pi}{L}(x+vt)\right\}\tag{34} \end{equation}$$

$f(x)$をFourier 正弦級数であらわした式(27)の変数$x$に$x-vt$と$x+vt$をそれぞれ代入すると、上式の右辺の$2$つの級数を得ます。すなわち、

$$\begin{equation} u(x,t)=\dfrac{1}{2}\biggl\{f^*(x-vt)+f^*(x+vt)\biggr\}\tag{35} \end{equation}$$

となります。但し、$f^*$は周期$2L$をもち、$f$を奇関数として拡張したものです（図3参照。）。図3では太字の赤線で描かれたグラフをもとにして、平行移動したものを細い赤線で、奇関数的に折り返したものを細い青線で描いています。初期変位$f(x)$が区間$0\leq x\leq L$で連続で、かつ両端点で$0$であるので、式(35)から$u(x,t)$は全ての$x$と$t$に対して連続です。また、式(35)を微分すると次のことが分かります。$f(x)$が区間$0<x<L$で$2$回微分可能で、かつ$x=0$と$x=L$で$2$階の片側微分係数（右微分係数または左微分係数）$0$を持てば、$u(x,t)$は式($\ref{8}$)の解です。従って、これらの条件の下で$u(x,t)$が式(9,10)を満たす式(8)の解であることが保証されます。

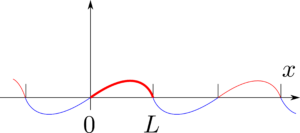
図3　$f(x)$の奇関数としての周期的拡張

式(35)の物理的解釈について考えてみましょう。図4のように、$f^*(x-vt)$のグラフは$f^*(x)$のグラフを右へ$vt$だけ移動させて得られます。従って、$f^*(x-vt)~(v>0)$は時間$t$の増加と共に右へ進行する波をあらわしています。同様に、$f^*(x+vt)$は左へ進行する波をあらわしています。つまり、$u(x,t)$はこれら$2$つの進行波の重ね合わせです。

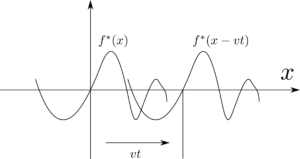
図4　式(35)の物理的解釈