$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$
問題
半径$R$の球の体積を求めよ。
解説
\begin{align}
V&=\int\rmd\tau=\int^R_{r=0}\int^\pi_{\theta=0}\int^{2\pi}_{\phi=0}r^2\sin{\theta}\rmd r\rmd\theta\rmd\phi\nonumber\\
&=\left(\int^R_0r^2\rmd r\right)\left(\int^\pi_0\sin{\theta}\rmd\theta\right)\left(\int^{2\pi}_0\rmd\phi\right)\nonumber\\
&=\left(\dfrac{R^3}{3}\right)\times2\times2\pi=\dfrac{4}{3}\pi R^3\nonumber
\end{align}
と計算することが出来る。これは既によく知っている球の体積の公式に他ならない。
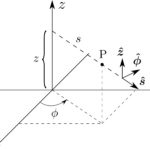
これまでのところ、我々は極座標の幾何学的なことについてのみ議論をしてきた。ここで、話をベクトルの微分、すなわち、極座標系$(r,\theta,\phi)$での勾配、発散、回転、そしてLaplacian に話を移そう。これは原理的にはすぐ実行することが出来る。勾配の場合は
\[
\nabla T=\dfrac{\partial T}{\partial x}\hbx+\dfrac{\partial T}{\partial y}\hby+\dfrac{\partial T}{\partial z}\hbz
\]
に連鎖律を適用して、例えば以下のように微分を展開する。
\[
\dfrac{\partial T}{\partial x}=\dfrac{\partial T}{\partial r}\left(\dfrac{\partial r}{\partial x}\right)+\dfrac{\partial T}{\partial \theta}\left(\dfrac{\partial \theta}{\partial x}\right)+\dfrac{\partial T}{\partial \phi}\left(\dfrac{\partial \phi}{\partial x}\right)
\]
括弧の中の項は(62)あるいはその逆関数から導くことが出来る。従って、$\partial T/\partial y$や$\partial T/\partial z$も同様にして計算することが出来る。そして、最後に$\hbx$、$\hby$、$\hbz$における勾配の式を$\hbr$、$\hbtheta$、$\hbphi$を用いて書き換える。この強引な方法で極座標における勾配の式を理解するのは$1$時間くらいの時間を要することになるだろう。ここでは初学者に曖昧さや誤魔化しなく計算過程を説明するために、直接的に導出する方法を述べた。これによって、異なる座標系でも勾配や発散などの量を計算することが出来るから、議論はこれで尽きていることになる。
これによって、極座標系におけるベクトルの微分は以下のようにまとめることが出来る。
- 勾配
\begin{equation}
\nabla T=\dfrac{\partial T}{\partial r}\hbr+\dfrac{1}{r}\dfrac{\partial T}{\partial \theta}\hbtheta+\dfrac{1}{r\sin{\theta}}\dfrac{\partial T}{\partial \phi}\hbphi\tag{70}
\end{equation}
- 発散
\begin{equation}
\nabla\cdot\bmsv=\dfrac{1}{r^2}\dfrac{\partial}{\partial r}(r^2v_r)+\dfrac{1}{r\sin{\theta}}\dfrac{\partial}{\partial\theta}(\sin{\theta}v_\theta)+\dfrac{1}{r\sin{\theta}}\dfrac{\partial v_\phi}{\partial \phi}\tag{71}
\end{equation}
- 回転
\begin{equation}
\nabla\times\bmsv=\dfrac{1}{r\sin{\theta}}\left[\dfrac{\partial}{\partial\theta}(\sin{\theta}v_\phi)-\dfrac{\partial v_\theta}{\partial\phi}\right]\hbr+\dfrac{1}{r}\left[\dfrac{1}{\sin{\theta}}\dfrac{\partial v_r}{\partial\phi}-\dfrac{\partial}{\partial r}(rv_\phi)\right]\hbtheta+\dfrac{1}{r}\left[\dfrac{\partial}{\partial r}(rv_\theta)-\dfrac{\partial v_r}{\partial\theta}\right]\hbphi\tag{72}
\end{equation}
- Laplacian
\begin{equation}
\nabla^2T=\dfrac{1}{r^2}\dfrac{\partial}{\partial r}\left(r^2\dfrac{\partial T}{\partial r}\right)+\dfrac{1}{r^2\sin{\theta}}\dfrac{\partial}{\partial\theta}\left(\sin{\theta}\dfrac{\partial T}{\partial\theta}\right)+\dfrac{1}{r^2\sin{\theta}}\dfrac{\partial^2T}{\partial\phi^2}\tag{73}
\end{equation}