$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$

円柱座標系

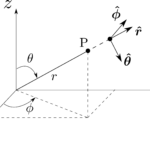
点P に対する円柱座標系$(s,\phi,z)$の定義は図1.42に与えられている通りである。ここでの$\phi$は極座標系での$\phi$と同じ意味を持っていること、更に$z$も直交座標系での$z$と同じ意味を持っているということに注意せよ。極座標系での$r$が原点から点P までの距離をあらわしていたのと同じように、ここでの$s$は$z$軸からの点P の距離をあらわしている。直交座標系と円柱座標系の関係は以下のように得られる。

\begin{equation}
x=s\cos{\phi},~y=s\sin{\theta},~z=z\tag{74}
\end{equation}

このときの単位ベクトルは以下で与えられる。

\begin{equation}
\left\{
\begin{array}{lcl}
\hbs&=&\cos{\phi}\hbx+\sin{\phi}\hby\\
\hbphi&=&-\sin{\phi}\hbx+\cos{\phi}\hby\\
\hbz&=&\hbz
\end{array}
\right.
\tag{75}
\end{equation}

そして微小変位は以下で与えられる。

\begin{equation}
\rmd l_s=\rmd s,~\rmd l_\phi=s\rmd\phi,~\rmd l_z=\rmd z\tag{76}
\end{equation}

故に、微小変位ベクトルを単位ベクトル$\hbs$、$\hbphi$、$\hbz$であらわすと

\begin{equation}
\rmd\bmsl=\rmd s\hbs+s\rmd\phi\hbphi+\rmd z\hbz\tag{77}
\end{equation}

となり、微小体積要素は

\begin{equation}
\rmd\tau=s\rmd s\rmd\phi\rmd z\tag{78}
\end{equation}

となる。$s$は$0$から$\infty$までの範囲、$\phi$は$0$から$2\pi$の範囲、$z$は$-\infty$から$+\infty$の範囲を取る。

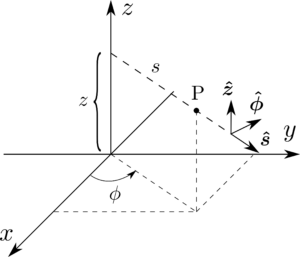
図1.42

これによって、極座標系におけるベクトルの微分は以下のようにまとめることが出来る。

勾配

\begin{equation}
\nabla T=\dfrac{\partial T}{\partial s}\hbs+\dfrac{1}{s}\dfrac{\partial T}{\partial\phi}+\dfrac{\partial T}{\partial z}\hbz\tag{79}
\end{equation}

発散

\begin{equation}
\nabla\cdot\bmsv=\dfrac{1}{s}\dfrac{\partial}{\partial s}(sv_s)+\dfrac{1}{s}\dfrac{\partial v_\phi}{\partial\phi}+\dfrac{\partial v_z}{\partial z}\tag{80}
\end{equation}

回転

\begin{equation}
\nabla\times\bmsv=\left(\dfrac{1}{s}\dfrac{\partial v_z}{\partial\phi}-\dfrac{\partial v_\phi}{\partial z}\right)\hbs+\left(\dfrac{\partial v_s}{\partial z}-\dfrac{\partial v_z}{\partial s}\right)\hbphi+\dfrac{1}{s}\left[\dfrac{\partial}{\partial s}(sv_\phi)-\dfrac{\partial v_s}{\partial \phi}\right]\hbz\tag{81}
\end{equation}

Laplacian

\begin{equation}
\nabla^2T=\dfrac{1}{s}\dfrac{\partial}{\partial s}\left(s\dfrac{\partial T}{\partial s}\right)+\dfrac{1}{s^2}\dfrac{\partial^2T}{\partial\phi^2}+\dfrac{\partial^2T}{\partial z^2}\tag{82}
\end{equation}