$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$

曲線座標系

極座標系

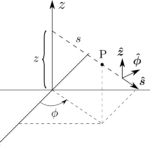
ある点$P$を直交座標系$(x,y,z)$であらわしても良いが、原点からの距離$r$、$z$軸からの角度をあらわす極角$\theta$、$x$軸からの角度をあらわす方位角$\phi$を用いた極座標系（polar coordinates）で点の位置をあらわす方がより便利となる。図1.36のように、極座標系と直交座標系の関係は以下の式で与えられる。

\begin{equation}
x=r\sin{\theta}\cos{\phi},~y=r\sin{\theta}\sin{\phi},~z=r\cos{\theta}\tag{62}
\end{equation}

更に、図1.36のように対応する座標の増加する向きを向いた$3$つの単位ベクトル$\hbr$、$\hbtheta$、$\hbphi$が存在する。これらは直交基底、すなわち、それぞれが直交しているようなベクトルのセットをなしており、$\hbx,\hby,\hbz$を用いたときと同様に、任意のベクトル$\bma$はこれらの基底を用いて以下のようにあらわすことが出来る。

\begin{equation}
\bma=A_r\hbr+A_\theta\hbtheta+A_\phi\hbphi\tag{63}
\end{equation}

$A_r,A_\theta,A_\phi$はそれぞれ$\bma$の動径成分、極成分、方位成分である。極座標系の基底は直交座標系の単位ベクトルを用いて、

\begin{equation}
\left\{
\begin{array}{lcl}
\hbr&=&\sin{\theta}\cos{\phi}\hbx+\sin{\theta}\sin{\phi}\hby+\cos{\theta}\hbz\\
\hbtheta&=&\cos{\theta}\cos{\phi}\hbx+\cos{\theta}\sin{\phi}\hby-\sin{\theta}\hbz\\
\hbphi&=&-\sin{\phi}\hbx+\cos{\phi}\hby
\end{array}
\right.
\tag{64}
\end{equation}

と書くことが出来る。このことは演習問題で確認することになる。

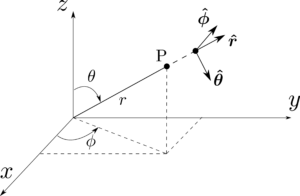
図1.36

しかし、これには初学者が陥りやすい間違いがあるのでそれについて言及しておく。$\hbr$、$\hbtheta$、$\hbphi$は特定の点P に関連していて、この点P が動く度に向きが変化する。例えば、$\hbr$は常に動径外向きを向いているが、この向きが$x$軸方向なのか、$y$軸方向なのか、$z$軸方向なのかはこの点が今どこにいるのかによって異なる。図1.37では$\bma=\hby$、$\bmb=-\hby$であるがどちらも極座標系での$\hbr$について書かれている。このことを考慮すると、参照している点を明示的に$\hbr(\theta,\phi)$、$\hbtheta(\theta,\phi)$、$\hbphi(\theta,\phi)$と記すことが出来るが、このように一々書くのは面倒であるし、一度理解しておけば困難に陥ることはないと思うので、今後は一々このようには書かない。特に、極座標系において異なる点でのベクトルの成分を素朴に足し合わせようとしてはいけない。図1.37で言えば、$\bma+\bmb$は$\bm{0}$であって$2\hbr$ではない。$\bma\cdot\bmb$も$-1$であって$1$とはならない。単位ベクトル自体は一の関数であるため、極座標であらわされるベクトルを微分するときは注意が必要である。例えば、$\partial\hbr=\partial\theta=\hbtheta$などとなる。また、(53)の$\hbx$、$\hby$、$\hbz$のようにして$\hbr$、$\hbtheta$、$\hbphi$を積分の外に出してはいけない。一般に、もし演算の妥当性が不明確なのであれば直交座標系に書き直せば良い。直交座標では上記のような困難は起こらない。

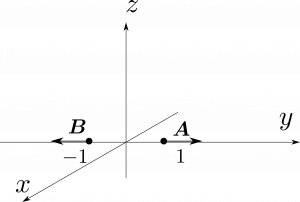
図1.37

図1.38(a)のように、$x$方向の微小変位が$\rmd x$であるのと同様に、$\hbr$方向の微小変位は単純に$\rmd r$である。

\begin{equation}
\rmd l_r=\rmd r\tag{65}
\end{equation}

一方で、図1.38(b)のように、$\hbtheta$方向の微小変位は単に$\rmd \theta$ではない。これは角度であって正しい次元になっていない。図を見れば分かるように、

\begin{equation}
\rmd l_\theta=r\rmd\theta\tag{66}
\end{equation}

である。同様に、図1.38(c)から、$\hbphi$方向の微小変位は以下のようになる。

\begin{equation}
\rmd l_\phi=r\sin{\theta}\rmd\phi\tag{67}
\end{equation}

結局、一般の微小変位$\rmd\bmsl$は以下のようになる。

\begin{equation}
\rmd\bmsl=\rmd r\hbr+r\rmd\theta\hbtheta+r\sin{\theta}\rmd\phi\hbphi\tag{68}
\end{equation}

これは例えば線積分では直交座標における微小変位$\rmd\bmsl=\rmd\hbx+\rmd\hby+\rmd\hbz$と同じ役割を果たす。

極座標における微小体積要素$\rmd\tau$は$3$つの微小変位の積で与えられる。

\begin{equation}
\rmd\tau=\rmd l_r\rmd l_\theta\rmd l_\phi=r^2\sin{\theta}\rmd r\rmd \theta\rmd\phi\tag{69}
\end{equation}

これらに対して、微小面積要素については一般の式を得ることが出来ない。面の向きづけに不定性があるためである。直交座標系や曲線座標系などと同様に、任意の場合において、簡単に幾何的状況を解析する必要がある。もし例えば球面上で面積分するなら、$r$は一定なので、図1.39のように

\[
\rmd\bmsa_1=\rmd l_theta\rmd l_\phi\hbr=r^2\sin{\theta}\rmd\theta\rmd\phi\hbr
\]

となる。一方で、$xy$平面上で面積分するなら、$\theta=\frac{\pi}{2}$で一定だから、$r$と$\phi$が変化して以下のようになる。

\[
\rmd\bmsa_2=\rmd l_r\rmd l_\phi\hbtheta=r\rmd r\rmd\phi\hbtheta
\]

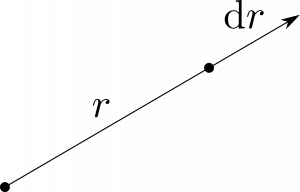
図1.38(a)

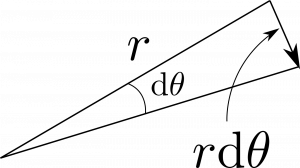
図1.38(b)

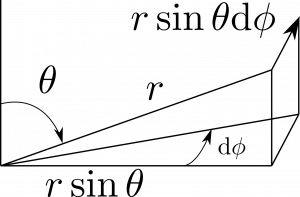
図1.38(c)

最後に、$r$は$0$から$\infty$までの範囲、$\phi$は$0$から$2\pi$の範囲、$\theta$は$0$から$\pi$の範囲を取るということに注意しておく。$\theta$が$2\pi$まで変化しないことに特に注意せよ。$2\pi$まで変化してしまうとダブルカウントになってしまう（代わりに、$\phi$を$0$から$\pi$まで変化させて東半分だけ覆って、$\theta$を$0$から$2\pi$まで変化させて西半分も覆うようにすることも出来る。しかし、これはとても悪いノーテーションである。何よりも$\sin{\theta}$が負になってしまうことがまずい。面積は体積は本質的に正の値を持つ必要があるから、体積要素や面積要素を考えたときに、$\sin{\theta}$が現れるたびに絶対値記号を用いる必要が生じてしまうためである。）。

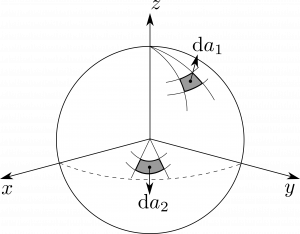
図1.39