$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

回転

ナブラ演算子の定義から、回転を次のように定義する。

$$\begin{align} \nabla\times\bmsv&=\left| \begin{array}{ccc} \hbx&\hby&\hbz\\ \partial/\partial x&\partial/\partial y&\partial/\partial z\\ v_x&v_y&v_z \end{array} \right|\nonumber\\ =&\hbx\left(\dfrac{\partial v_z}{\partial y}-\dfrac{\partial v_y}{\partial z}\right)+\hby\left(\dfrac{\partial v_x}{\partial z}-\dfrac{\partial v_z}{\partial x}\right)+\hbz\left(\dfrac{\partial v_y}{\partial x}-\dfrac{\partial v_x}{\partial y}\right)\tag{41} \end{align}$$

ベクトル関数$\bmsv$の回転$\nabla\times\bmsv$はベクトルとなることに注意せよ（スカラー関数の回転のようなものは存在しない。）。

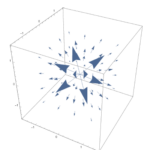
幾何学的には、回転という名前は上手くつけられていて、$\nabla\times\bmsv$はベクトル$\bmsv$が考えている点の周りでどれくらい渦を巻くかをあらわしている。

従って、以前の図1.18の$3$つの図はどれも回転が$\bm{0}$であることが直ちに確認出来る。

これに対して、図1.19の$2$つの図は$z$方向の周りで回転があり、その向きは右ねじを回す向きになっている。再び池の縁に立っている姿を想像してみよう。

近くに小さな歯車を浮かべてみて、それが回転したならあなたが立っているところの周りには$\bm{0}$でない回転があるということになる。渦巻きが目に見えて出来ているところは、特に回転が大きいところである。

図1.19(a)

図1.19(b)

問題

図19の関数はそれぞれ、$\bmsv_a=-y\hbx+x\hby$、$\bmsv_b=x\hby$である。これらの回転をそれぞれ計算せよ。

解説

以下のように計算する。

$$\nabla\times\bmsv_a= \left| \begin{array}{ccc} \hbx&\hby&\hbz\\ \partial/\partial x&\partial/\partial y&\partial/\partial z\\ -y&x&0 \end{array} \right| =2\hbz$$

$$\nabla\times\bmsv_b= \left| \begin{array}{ccc} \hbx&\hby&\hbz\\ \partial/\partial x&\partial/\partial y&\partial/\partial z\\ 0&x&0 \end{array} \right| =\hbz$$

予想していたように、これらは$+z$方向への回転となっている。また、これらには発散がない。これも予想していた結果であるから、それぞれ理にかなっている結果である。

積法則

常微分の計算は計算法則を導入することで容易に実行出来るようになる。和法則は以下のような式になる。

$$\dfrac{\rmd}{\rmd x}(f+g)=\dfrac{\rmd f}{\rmd x}+\dfrac{\rmd g}{\rmd x}$$

定数$k$を掛けた場合の法則は次のとおりである。

$$\dfrac{\rmd}{\rmd x}(kf)=k\dfrac{\rmd f}{\rmd x}$$

積法則は次のとおりである。

$$\dfrac{\rmd}{\rmd x}(fg)=f\dfrac{\rmd g}{\rmd x}+g\dfrac{\rmd f}{\rmd x}$$

そして商法則は以下のようになる。

$$\dfrac{\rmd}{\rmd x}\left(\dfrac{f}{g}\right)=\dfrac{g\dfrac{\rmd f}{\rmd x}-f\dfrac{\rmd g}{\rmd x}}{g^2}$$

同じような関係式がベクトルの微分でも成り立つ。従って、以下のような$6$つの式が成り立つ。

$$\left\{ \begin{array}{lcl} \nabla(f+g)&=&\nabla f+\nabla g\\ &&\\ \nabla\cdot(\bma+\bmb)&=&(\nabla\cdot\bma)+(\nabla\cdot\bmb)\\ &&\\ \nabla\times(\bma+\bmb)&=&(\nabla\times\bma)+(\nabla\times\bmb)\\ &&\\ &&\\ \nabla(kf)&=&k\nabla f\\ &&\\ \nabla\cdot(k\bma)&=&k(\nabla\cdot\bma)\\ &&\\ \nabla\times(k\bma)&=&k(\nabla\times\bma) \end{array} \right.$$

これらが成り立つことは直ちに計算して確かめることが出来る。但し、積法則はこれほど単純ではない。スカラーを構成する方法は$2$つのスカラーの積$fg$と$2$つのベクトルの内積$\bma\cdot\bmb$という$2$通りあるし、ベクトルを構成する方法も$1$つのスカラーと$1$つのベクトルの積$f\bma$と$2$つのベクトルの外積$\bma\times\bmb$という$2$通りがあるためである。

このような状況によって、$6$つの積法則が成り立つことになる。勾配についての法則、発散についての法則、回転についての法則がそれぞれ$2$つずつとなっている。

(1)$\nabla(fg)=f\nabla g+g\nabla f$

(2)$\nabla(\bma\cdot\bmb)=\bma\times(\nabla\times\bmb)+\bmb\times(\nabla\times\bma)+(\bma\cdot\nabla)\bmb+(\bmb\cdot\nabla)\bma$

(3)$\nabla\cdot(f\bma)=f(\nabla\cdot\bma)+\bma\cdot(\nabla f)$

(4)$\nabla\cdot(\bma\times\bmb)=\bmb\cdot(\nabla\times\bma)-\bma\cdot(\nabla\times\bmb)$

(5)$\nabla\times(f\bma)=f(\nabla\times\bma)-\bma\times(\nabla f)$

(6)$\nabla\times(\bma\times\bmb)=(\bmb\cdot\nabla)\bma-(\bma\cdot\nabla)\bmb+\bma(\nabla\cdot\bmb)-\bmb(\nabla\cdot\bma)$

これらの規則は非常に頻繁に使うことになる。これらの式が成り立つことの証明は非常に簡単で、実際に計算してみればよい。例えば、以下のように計算する。

$$\begin{align} \nabla\cdot(f\bma)=&\dfrac{\partial}{\partial x}(fA_x)+\dfrac{\partial}{\partial y}(fA_y)+\dfrac{\partial}{\partial z}(fA_z)\nonumber\\ =&\left(\dfrac{\partial f}{\partial x}A_x+f\dfrac{\partial A_x}{\partial x}\right)+\left(\dfrac{\partial f}{\partial y}A_y+f\dfrac{\partial A_y}{\partial y}\right)+\left(\dfrac{\partial f}{\partial z}A_z+f\dfrac{\partial A_z}{\partial z}\right)\nonumber\\ =&(\nabla f)\cdot\bma+f(\nabla\cdot\bma) \end{align}$$

同様に以下の$3$つの商法則も定式化することが出来る。

$$\left\{ \begin{array}{rcl} \nabla\left(\dfrac{f}{g}\right)&=&\dfrac{g\nabla f-f\nabla g}{g^2}\\ &&\\ \nabla\cdot\left(\dfrac{\bma}{g}\right)&=&\dfrac{g(\nabla\cdot\bma)-\bma\cdot(\nabla g)}{g^2}\\ &&\\ \nabla\times\left(\dfrac{\bma}{g}\right)&=&\dfrac{g(\nabla\times\bma)-\bma\times(\nabla g)}{g^2} \end{array} \right.$$

しかし、これらは積法則から直ちに得られるので、あえて積法則と分けて述べるべき要点はない。