$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

$3$次元におけるDirac のデルタ関数

前回は$1$次元のデルタ関数について議論した。
実際に電磁気学で必要になるのは$3$次元のデルタ関数であるから、$3$次元への拡張を議論しよう。
デルタ関数は容易に$3$次元に拡張することが出来る。

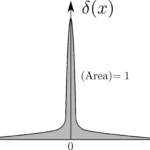
通常、$\bmsr\coloneqq x\hbx+y\hby+z\hbz$は原点から点$(x,y,z)$にかけて伸びる位置ベクトルである。$3$次元のデルタ関数は原点$(0,0,0)$を除く全ての点で$0$であり、体積積分すると$1$となる。

また、(92)の一般化で以下が成り立つ。

$1$次元のデルタ関数と同様、デルタ関数$\delta^3(\bmsr-\bmsa)$と共に積分するとデルタ関数のトゲの位置における関数$f(\bmsr)$の値を抜き出すことが出来る。

我々はここで、以前導入を行ったパラドックスを再考することにしよう。以前やったように、$\hbr/r^2$の発散は原点以外のいたるところで$0$となるが、原点を含む任意の領域で体積積分を行うと値が$4\pi$という定数になる。これらの問題はDirac のデルタ関数を用いて条件の定義を行うことが出来て、

となる。より一般には、間隔ベクトル$\bcar\coloneqq\bmsr-\bmsr’$を用いて

となる。ここでの微分は$\bmsr$に関するものであって、$\bmsr’$は定ベクトルであるということに注意せよ。更に、

という式が成り立つので、以下のような関係式も得ることが出来る。

問題

以下の積分を計算せよ。但し、$\mathcal{V}$は中心が原点にあるような半径$R$の球である。

ここで、球という用語について注意をしておく。数学的に正確な用語としては、sphere は球面を指していて、ball は球内の体積も含んでいる。しかし、物理学者はこれらをいずれも球と呼ぶことが多い。文脈から球面なのか球体なのかが明確に推測できない場合は球の面や球面の体積などと使い分けることにするが、特に問題が無ければ球と書くことにする。言葉に厳しい人にとっては、球の面というのはしつこく聞こえるかもしれないし、球面の体積というのも矛盾した言葉であるように感じるかもしれないが、物理学者はこれらを普通に使用している。

解説1

発散を書き直すために(99)を用いて、積分を実行するために(98)を用いると、

となる。この直観的な方法はデルタ関数が便利で美しいものであるということを示しているだろうが、この後に紹介する第$2$の解法も見てほしい。こちらはややこしい方法ではあるが、部分積分による方法を利用した興味深い解法である。

解説2

(59)を用いて、微分を$\hbr/r^2$から$(r^2+2)$へ書き換えて、

勾配は$\nabla(r^2+2)=2r\hbr$であるから、体積積分は

となる。一方で、球面（$r=R$）では$\rmd\bmsa=R^2\sin{\theta}\rmd\theta\rmd\phi\hbr$なので、面積分は

となる。これらを代入すれば、

となり先ほどの解説1と同じ値が得られることになる。