$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

前回は電磁波の放出(輻射)について扱いましたが、今回も引き続いて輻射の問題と解説について紹介していきます。

問題

[問題1]荷電粒子が等速直線運動する場合、荷電粒子が作る電磁場を求め、特徴を説明せよ。
[問題2]$\dot{\bm{r}}_0\parallel\ddot{\bm{r}}_0$の場合（制動放射）、放出される輻射の強度分布（$|\bm{E}|^2$の方向依存性）を議論せよ。
[問題3]$\dot{\bm{r}}\perp\ddot{\bm{r}}_0$で荷電粒子が等速円運動をする場合、$\beta\ll1$として輻射の強度分布を論ぜよ（サイクロトロン輻射）。
[問題4]問題3において、$\beta\simeq1$の場合の輻射の強度分布を論ぜよ（シンクロトロン輻射）。

演習問題解答

[問題1]
$\dot{\bm{r}}_0=\bm{0}$のときに荷電粒子によって作られる電場及び磁束密度は
$$\left\{ \begin{array}{l} \bm{E}=\displaystyle\frac{Q}{4\pi\varepsilon_0}\frac{1}{\gamma^2s^3}\left\{(\bm{R}-R\bm{\beta})+\frac{\gamma^2}{c^2}\bm{R}\times\left[(\bm{R}-R\bm{\beta})\times\ddot{\bm{r}}_0\right]\right\}\\ \\ \bm{B}=\displaystyle\frac{1}{c}\frac{\bm{R}}{R}\times\bm{E}\\ ~ \end{array} \right.$$
を用いて計算するとただちに以下のように求めることが出来る。
$$\left\{ \begin{array}{l} \bm{E}=\displaystyle\frac{Q}{4\pi\varepsilon_0}\frac{1}{\gamma^2s^3}(\bm{R}-R\bm{\beta})　\left(\propto\displaystyle\frac{1}{R^2}　\mathrm{for}~R\gg1\right)\\ \\ \bm{B}=\displaystyle\frac{\mu_0Q}{4\pi}\frac{1}{\gamma^2s^3}(\dot{\bm{r}}_0\times\bm{R})　\left(\propto\displaystyle\frac{1}{R^2}　\mathrm{for}~R\gg1\right)\\ ~ \end{array} \right.$$
これを用いるとPoynting ベクトルは以下のように求まる。
$$\bm{S}=\displaystyle\frac{1}{c\mu_0}|\bm{E}|^2\frac{\bm{R}}{R}=\frac{c\mu_0Q^2}{16\pi^2}\frac{R^2}{\gamma^4s^6}\left|\frac{\bm{R}}{R}-\bm{\beta}\right|^2\frac{\bm{R}}{R}　\left(\propto\displaystyle\frac{1}{R^4}　\mathrm{for}~R\gg1\right)$$
よってPoynting ベクトルは$R\rightarrow\infty$で$\bm{S}\rightarrow\bm{0}$となるから、荷電粒子が等速直線運動する場合、荷電粒子が作る電磁場は無限遠へエネルギーを放出することはないと結論出来る。

因みに、初めの方に求めた電場及び磁束密度はLorentz 変換を用いて計算できる等速直線運動する電荷が作る電場及び磁束密度に一致している。以下、これについて追加で考察してみることにする。電荷$Q$の荷電粒子の静止系で電場及び磁束密度は
$$\left\{ \begin{array}{l} \bm{E}’=\displaystyle\frac{Q}{4\pi\varepsilon_0}\frac{\bm{R}’}{R’^3}\\ \\ \bm{B}’=\bm{0}\\ ~ \end{array} \right.$$
である。先に導いた「無限遠へエネルギーを放出することはない」という結論はここからも確認出来るであろう。さて、これを$\bm{u}=-\dot{\bm{r}}_0$で等速直線運動する系へLoretz 変換すると
$$\left\{ \begin{array}{l} \bm{E}=\displaystyle\frac{Q}{4\pi\varepsilon_0R’^3}\frac{\bm{R}-\dot{\bm{r}}_0t}{\sqrt{1-\beta^2}}=\displaystyle\frac{Q}{4\pi\varepsilon_0}\frac{1}{\gamma^2s^3}(\bm{R}-R\bm{\beta})\\ \\ \bm{B}=\displaystyle\frac{\mu_0Q}{4\pi R’^3}\frac{\dot{\bm{r}}_0\times\bm{R}’}{\sqrt{1-\beta^2}}=\displaystyle\frac{\mu_0Q}{4\pi}\frac{1}{\gamma^2s^3}(\dot{\bm{r}}_0\times\bm{R})\\ ~ \end{array} \right.$$
と求まる。但し、それぞれ$R’=\gamma s$という関係式を用いた。これらは確かに先に行った計算結果に一致している。

[問題2]
$\dot{\bm{r}}_0\parallel\ddot{\bm{r}}_0$のとき荷電粒子から放射される電場は
$$\bm{E}=\displaystyle\frac{Q}{4\pi\varepsilon_0 c^2}\frac{1}{s^3}\bm{R}\times(\bm{R}\times\ddot{\bm{r}}_0)$$
よって$|\bm{E}|^2$は以下の通り。また、$\displaystyle\frac{\sin^2{\theta}}{(1-\beta\cos{\theta})^6}$の角度分布を$\theta$の関数として図1に示す。
$$|\bm{E}|^2=\displaystyle\left(\frac{Q}{4\pi\varepsilon_0 c^2}\right)^2\frac{|\ddot{\bm{r}}_0|^2\sin^2{\theta}}{R^2(1-\beta\cos{\theta})^6}$$
この図から荷電粒子の放射エネルギーについて次のことが言える。まず、$\beta$が$1$に近づくと、速度・加速度ベクトルの前方方向の放射エネルギーが増大する。但し、超前方$\theta\simeq0$では放射は0となる。また、$\theta={90}^\circ$では$\cos{\theta}=0$だから放射エネルギーは$\beta$に依存しない。そして、$\beta\rightarrow1$では$\theta=(2\gamma)^{-1}$にピークが現れる。

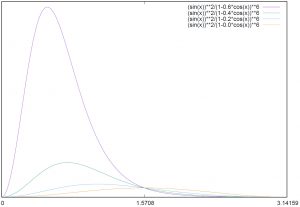
速度と平行に加速される荷電粒子による$|\bm{E}^2|$の角度分布

[問題3]
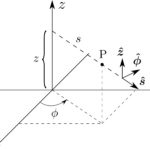
$\dot{r}_0$が$z$軸、$\ddot{r}_0$が$x$軸となるように座標軸をとり、$x$軸と$\bm{R}$のなす角を$\Theta$とすると、
$$\begin{align} |\bm{R}\times[(\bm{R}-R\bm{\beta})\times\ddot{r}_0]|^2=&R^4\{(1-\beta\cos{\theta})^2\ddot{r}_0^2-(1-\beta^2)\ddot{r}_0^2\cos^2{\Theta}\nonumber\\ =&R^4\{(1-\beta\cos{\theta})^2\ddot{r}_0^2-(1-\beta^2)\ddot{r}_0^2\sin^2{\theta}\cos^2{\phi}\} \end{align}$$
となる。但し、ここで極座標で$(\theta_1,\phi_1)$方向と$(\theta_2,\phi_2)$方向のなす角を$\Theta$としたときに球面三角法により球面加法定理$\cos{\Theta}=\cos{\theta_1}\cos{\theta_2}+\sin{\theta_1}\sin{\theta_2}\cos{(\phi_1-\phi_2)}$が成り立つことを用いた（$\theta_2=\frac{\pi}{2}$、$\phi_2=0$を代入すれば$\cos{\Theta}=\sin{\theta}\cos{\phi}$を得る。）。これらの結果を用いると$|\bm{E}|^2$の値は以下のように求められる。
$$|\bm{E}|^2=\displaystyle\left(\frac{Q}{4\pi\varepsilon_0 c^2}\right)^2\frac{(1-\beta\cos{\theta})^2\ddot{r}_0^2-(1-\beta^2)\ddot{r}_0^2\sin^2{\theta}\cos^2{\phi}}{R^2(1-\beta\cos{\theta})^6}$$
特にサイクロトロン放射の場合、$\beta=0$とおけば
$$|\bm{E}|^2=\displaystyle\left(\frac{Q}{4\pi\varepsilon_0 c^2}\right)^2\frac{\ddot{r}_0^2\sin^2{\Theta}}{R^2}$$
となり観測方向と加速度方向のなす角の正弦の$2$乗に比例することが分かる。

[問題4]
問題3の式を用いると、特にシンクロトロン放射の場合、相対論効果によって強度分布が前方に著しく傾き狭い範囲に集中して放射される。これより$\theta=0$の周りで展開して$\beta=1$、$1-\beta=(2\gamma^2)^{-1}$とおけば
$$|\bm{E}|^2=\displaystyle\left(\frac{Q}{4\pi\varepsilon_0 c^2}\right)^2\frac{16\gamma^8\ddot{r}_0^2}{R^2}(1-4\gamma^2\theta^2\cos^2{\phi})$$
となり輻射が$\theta=0$の近傍に集中していることが分かる。

参考文献

[1]渡辺誠、佐藤繁『放射光科学入門』、東北大学出版会、2010
[2]岡真『電磁場の古典論』、培風館、2009