$\def\bm#1{{\boldsymbol{#1}}}$
$\def\rmd#1{\mathrm{d}{#1}}$
$\def\Braket#1{\langle{#1}\rangle}$
$\def\Bra#1{\langle{#1}|}$
$\def\Ket#1{|{#1}\rangle}$
$\def\kb{k_{\text{B}}}$
$\def\dag{\dagger}$

物理学実験

電気回路の基礎

交流$V=V_0\mathrm{e}^{i\omega t}$におけるインピーダンス$Z$に対して以下が成り立つ。
\begin{equation}
\left\{
\begin{array}{rcl}
\text{Capacitor}:Z&=&1/(i\omega C)\\
\text{Inductor}:Z&=&i\omega L\\
\text{Resistor}:Z&=&R
\end{array}
\right.
\end{equation}
このとき、オームの法則$V=IZ$が成り立ち、以下のように合成ができる。
\begin{equation}
\left\{
\begin{array}{rcl}
\text{Series}:Z_{\text{tot}}&=&Z_1+\cdots+Z_n\\
\text{Parallel}:Z_{\text{tot}}^{-1}&=&Z_1^{-1}+\cdots+Z_n^{-1}
\end{array}
\right.
\end{equation}

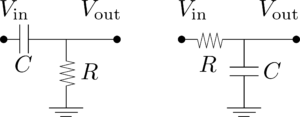
ハイパスフィルター

左図のように抵抗$R$が設置されている場合、高周波数では抵抗のインピーダンスが支配的となり、コンデンサー$C$の前後での電圧降下は無視できる。つまり、高周波数は通過するが低周波数は減衰する。このようなフィルターをハイパスフィルターという。

ローパスフィルター

右図のようにコンデンサー$C$が設置されている場合、ハイパスフィルターとは逆の現象が起こる。つまり、低周波数は通過するが高周波数は減衰する。このようなフィルターをローパスフィルターという。

バンドパスフィルター

LC 回路のインピーダンスは
\begin{equation}
Z_{LC}=\dfrac{-i(1-\omega^2LC)}{\omega C}
\end{equation}
なので、$\omega=\omega_0=1/\sqrt{LC}$で$Z_{LC}=0$となる。このとき周波数$\omega_0$の近傍の物理現象のみが抽出される。このようなフィルターをバンドパスフィルターという。

ダイオード

ダイオードとは電流を一定方向にしか流さないような性質を持つ素子のことである。図の矢印の向きに流れると覚えれば良い。但し、バイアス電圧を超える電圧がかからない限り電流は流れない。典型的なシリコンダイオードの場合、バイアス電圧は$0.7~\text{V}$ほどである。ダイオードは交流を直流に変える際に利用される（これを整流回路と呼ぶ。）。また、電流の経路を変える際にも利用される。

オペアンプ

オペアンプ(Op-amp)とはoperational amplifier の略で、$2$つの入力端子と$1$つの出力端子を持つ素子のことである。出力電圧は$2$つの入力電圧の差に比例しており、比例定数は通常$10000$ほどである。しかし、オペアンプの最大出力電圧には上限があり、入力電圧差が大きくなると出力電圧は飽和してしまう。これをクリッピングと呼ぶ。

論理回路

論理回路は図のような$2$つの入力端子$A$、$B$と$1$つの出力端子$Z$からなるAND ゲートとOR ゲートなどからなる回路である。左図はAND ゲートであり、$Z=A~\text{AND}~B$である。中図はOR ゲートであり、$Z=A~\text{OR}~B$である。右図はNOT ゲートである。NOT ゲートは否定を意味しており、白丸$\circ$で描かれることもある。高出力電圧を$1$、低出力電圧を$0$として扱う。

論理の完備性により、NAND ゲートとNOR ゲートは自身を複数組み合わせることで任意の基本ゲートを作ることができる。