$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

積分学

電磁気学では、線積分（line integral）（線積分をpath integral と読んでいる本も散見されるが、量子力学などで現れる経路積分もpath integral と呼ぶので、混乱を避けるためここではline integral とした。）、面積分（surface integral）、体積積分（volume integrals）という種類の積分に頻繁に遭遇する。

線積分

線積分は次のような形式であらわされる。

$$\begin{equation} \int_{\bmsa}^{\bmsb}\bmsv\cdot\rmd\bmsl\tag{48} \end{equation}$$

但し、$\bmsv$はベクトル関数で、$\rmd\bmsl$は(22)の微小間隔ベクトルである。また、積分は図1.20にて矢印が記されている点$\bmsa$から点$\bmsb$までの積分路$\mathcal{P}$に沿って実行される。もし$\bmsa=\bmsb$となって始点と終点が一致している場合、以下のように積分に丸を書いて強調する。これを特に周積分という。

$$\begin{equation} \oint\bmsv\cdot\rmd\bmsl\tag{49} \end{equation}$$

これによって積分路の各点で$\bmsv$と微小間隔ベクトル$\rmd\bmsl$の内積$\bmsv\cdot\rmd\bmsl$を取る。物理をやる人にとって最も馴染みのある例は力$\bmf$がする仕事を計算するときの式$W=\int\bmf\cdot\rmd\bmsl$だろう。

通常だと線積分の値は$\bmsa$と$\bmsb$を結ぶ積分路の取り方に露わに依存するが、積分値が積分路の取り方に依存しない特別な場合も存在する（このような性質を持つ力のことを保存力（conservative force）という。）。我々は後にこのようなベクトルの特別なクラスを特徴づけることになる。

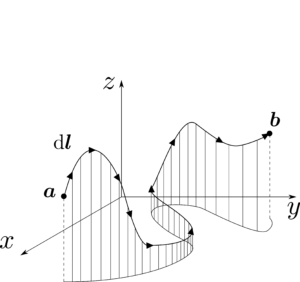
図1.20

問題

図1.21のベクトル関数$\bmsv=y^2\hbx+2x(y+1)\hby$の点$\bmsa=(1,1,0)$から点$\bmsb=(2,2,0)$を結んだ積分路(1)と積分路(2)に沿った線積分をそれぞれ計算せよ。また、積分路(1)から積分路(2)逆向き積分路を辿る周積分$\oint\bmsv\cdot\rmd\bmsl$はどのような値になるだろうか？

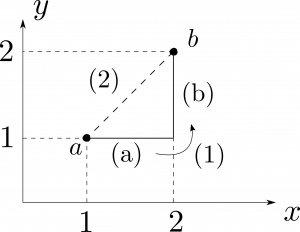
図1.21

解説

いずれの積分路でも$\rmd\bmsl=\rmd x\hbx+\rmd y\hby+\rmd z\hbz$を利用する。まず、積分路(1)は積分路(a)と積分路(b)に分けて計算すると良い。

積分路(a)は、$x$軸に平行な積分路なので$\rmd y=\rmd z=0$である。従って、$\rmd\bmsl=\rmd x\hbx$、$y=1$、$\bmsv\cdot\rmd\bmsl=y^2\rmd x=\rmd x$を用いれば、以下のようになる。

$$\int\bmsv\cdot\rmd\bmsl=\int^2_1\rmd x=1$$

積分路(b)は、$y$軸に平行な積分路なので$\rmd x=\rmd z=0$である。従って、$\rmd\bmsl=\rmd y\hby$、$x=2$、$\bmsv\cdot\rmd\bmsl=2x(y+1)\rmd y=4(y+1)\rmd y$を用いれば、以下のようになる。

$$\int\bmsv\cdot\rmd\bmsl=4\int^2_1(y+1)\rmd y=10$$

以上より、積分路(1)の線積分は、以下のようになる。

$$\int_{\bmsa}^{\bmsb}\bmsv\cdot\rmd\bmsl=1+10=11$$

これに対して、積分路(2)は、$x=y$なので$\rmd x=\rmd y$、$\rmd z=0$である。従って、$\rmd\bmsl=\rmd x\hbx+\rmd y\hby$、$\bmsv\cdot\bmsl=x^2\rmd x+2x(x+1)\rmd x=(3x^2+2x)\rmd x$を用いれば、積分路(2)の線積分は

$$\int_{\bmsa}^{\bmsb}\bmsv\cdot\rmd\bmsl=\int_1^2(3x^2+2x)\rmd x=(x^3+x^2)\biggr|_1^2=10$$

となる。ここでの戦略は$x=y$を利用して$x$だけで積分を表現するということにある。

これらより、求める周積分の値は以下のようになる。

$$\oint\bmsv\cdot\rmd\bmsl=11-10=1$$

面積分

面積分は次のような形式であらわされる。

$$\begin{equation} \int_\mathcal{S}\bmsv\cdot\rmd\bmsa\tag{50} \end{equation}$$

但し、ここでも$\bmsv$はベクトル関数であり、この積分は特徴づけられた積分面$\mathcal{S}$についての積分となる。ここで、$\rmd\bmsa$は図1.22のように積分面の一区画であり、積分面と垂直な方向を向いている。勿論、この方向には$2$つの可能性があるので、面積分は向きづけという内的な曖昧さを有している。もし風船のように積分面が閉じているのなら、先ほどのように、

$$\oint\bmsv\cdot\rmd\bmsa$$

という形で明示的に書く。このとき、外向きを正と採るのが慣習的であるが、開いた積分面については符号を任意に採れる。もし$\bmsv$が流体の流れ（単位は$[\mathrm{kg}/\mathrm{m}^2\cdot\mathrm{s}]$となる。）をあらわすなら、$\int\bmsv\cdot\rmd\bmsa$は単位時間あたりに断面を通り抜ける質量をあらわすので、流速（flux）と呼ばれる。

通常だと面積分の値は積分面の取り方に露わに依存するが、積分値が積分面の取り方に依存せず、境界線の取り方のみで値が決まるような特別な場合も存在する。我々は後にこのような関数の特別なクラスを特徴づけることになる。

図1.22

問題

ベクトル関数$\bmsv=2zx\hbx+(x+2)\hby+y(z^2-3)\hbz$について、図1.23のような各辺の長さが$2$の立方体について底面を除いた$5$つの面の面積分を計算せよ。正の向きは図の矢印が示すように上向き・外向きに採ること。

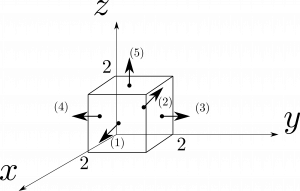
図1.23

解説

以下のように各面の面積分を計算する。
経路(1)

$$\int\bmsv\cdot\rmd\bmsa=4\int_0^2\rmd y\int_0^2z\rmd z=16$$

経路(2)

$$\int\bmsv\cdot\rmd\bmsa=0$$

経路(3)

$$\int\bmsv\cdot\rmd\bmsa=\int_0^2(x+2)\rmd x\int_0^2\rmd z=12$$

経路(4)

$$\int\bmsv\cdot\rmd\bmsa=-\int_0^2(x+2)\rmd x\int_0^2\rmd z=-12$$

経路(5)

$$\int\bmsv\cdot\rmd\bmsa=\int_0^2\rmd x\int_0^2y\rmd y=4$$

結局、全流束は以下のように得られる。

$$\int_{\mathrm{surface}}\bmsv\cdot\rmd\bmsa=16+0+12-12+4=20$$

体積積分

体積積分は次のような形式であらわされる。

$$\begin{equation} \int_\mathcal{V}T\rmd\tau\tag{51} \end{equation}$$

但し、$T$はスカラー関数であり、$\rmd\tau$は微小体積要素である。これは直交座標では、以下のように書ける。

$$\begin{equation} \rmd\tau=\rmd x\rmd y\rmd z\tag{52} \end{equation}$$

もし、$T$が各点によって値が異なるような物質の密度をあらわす場合、その体積積分は物質の質量となる。時折、我々はベクトル関数の体積積分にも遭遇するが、それは以下のように書くと約束されている。

$$\begin{equation} \int\bmsv\rmd\tau=\int(v_x\hbx+v_y\hby+v_z\hbz)\rmd\tau=\hbx\int v_x\rmd\tau+\hby\int v_y\rmd\tau+\hbz\int v_z\rmd\tau\tag{53} \end{equation}$$

$\hbx,\hby,\hbz$はそれぞれ単位ベクトルで定数のベクトルであるから、積分の外に出すことが出来る。

問題

図1.24のような三角柱について、スカラー関数$T=xyz^2$の体積積分を計算せよ。

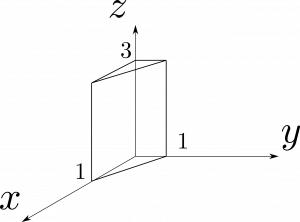
図1.24

解説

$x,y,z$の$3$つの積分を好きな順番で実行することになる。まず、$0$から$1-y$までの範囲で$x$についての積分を行って、次に$0$から$1$までの範囲で$y$についての積分を行って、最後に$0$から$3$までの範囲で$z$についての積分を行う。

$$\int T\rmd\tau=\int_0^3z^2\left\{\int_0^2y\left[\int_0^{1-y}x\rmd x\right]\rmd y\right\}\rmd z=\dfrac{1}{2}\int_0^3z^2\rmd z\int_0^1(1-y)^2y\rmd y=\dfrac{3}{8}$$