$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$
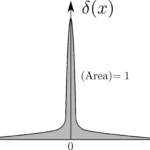
発散における基本定理
発散における基本定理は以下の式が成り立つことを主張している。
\begin{equation}
\int_\mathcal{V}(\nabla\cdot\bmsv)\rmd\tau=\oint_\mathcal{S}\bmsv\cdot\rmd\bmsa\tag{56}
\end{equation}
この式は非常に重要なので、敬意を表してGauss の定理(Gauss’s theorem)、Green の定理(Green’s theorem)、発散定理(divergence theorem)という$3$つの名前が付けられている。他の基本定理のように、この定理もある領域(今は体積$\mathcal{V}$)における導関数(今は発散)の積分は境界(今は体積$\mathcal{V}$の表面$\mathcal{S}$)での関数の値に等しいということをあらわしている。境界項はそれ自身が積分(今は面積分)になっているということに注意せよ。このことは、ある線の境界が$2$つの端点で定まるのに対して、体積の境界が閉局面になるということからも丁度良いということが伺える。
幾何学的には、もし$\bmsv$が非圧縮性流体の流れをあらわすとき、$\bmsv$の流束((56)の右辺)は単位時間当たりに表面を通過する流体の総量をあらわしている。今、発散は流体が注がれる蛇口に値するようなある点からのベクトルの湧き出しを測っている。非圧縮性の流体で満たされた領域に沢山の蛇口があったとすると、その領域の境界から同量の液体が押し出されることになる。実際には、その量を計算する方法は、それぞれの蛇口からどれぐらい注がれるのかを数えてそれらを足し合わせるというやり方と、境界の周りの各点でどれだけ押し出されるのかを測って足し合わせるという$2$通りが存在する。これによって、発散定理のエッセンスは以下のような主張であると言える。
\[
\int(考えている体積内の蛇口)=\oint(それぞれの面の流れ)
\]
問題
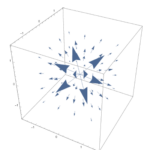
図1.29のように、各辺の長さが$1$の単位立方体を用いて、ベクトル関数$\bmsv=y^2\hbx+(2xy+z^2)\hby+(2yz)\hbz$について、発散における基本定理を確認せよ。
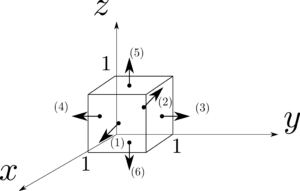
図1.29
解説
この場合、$\nabla\cdot\bmsv=2(x+y)$であり、
\[
\int_{\mathcal{V}}2(x+y)\rmd\tau=2\int_0^1\int_0^1\int_0^1(x+y)\rmd x\rmd y\rmd z
\]
\[
\int_0^1(x+y)\rmd x=\dfrac{1}{2}+y,~~~\int_0^1\left(\dfrac{1}{2}+y\right)=1,~~~\int_0^11\rmd z=1
\]
となる。従って、発散定理の左辺は以下のように計算出来る。
\[
\int_{\mathcal{V}}\nabla\cdot\bmsv\rmd\tau=2
\]
発散定理の右辺を計算するためには、各面で面積分を行って、その$6$面の結果を足し合わせればよい。
(1)
\[
\int\bmsv\cdot\rmd\bmsa=\int_0^1\int_0^1y^2\rmd y\rmd z=\dfrac{1}{3}
\]
(2)
\[
\int\bmsv\cdot\rmd\bmsa=-\int_0^1\int_0^1y^2\rmd y\rmd z=-\dfrac{1}{3}
\]
(3)
\[
\int\bmsv\cdot\rmd\bmsa=\int_0^1\int_0^1(2x+z^2)\rmd x\rmd z=\dfrac{4}{3}
\]
(4)
\[
\int\bmsv\cdot\rmd\bmsa=-\int_0^1\int_0^1z^2\rmd x\rmd z=-\dfrac{1}{3}
\]
(5)
\[
\int\bmsv\cdot\rmd\bmsa=\int_0^1\int_0^12y\rmd x\rmd y=1
\]
(6)
\[
\int\bmsv\cdot\rmd\bmsa=-\int_0^1\int_0^10\rmd x\rmd y=0
\]
故に、全流束は以下のように計算出来る。
\[
\oint_{\mathcal{S}}\bmsv\cdot\rmd\bmsa=\dfrac{1}{3}-\dfrac{1}{3}+\dfrac{4}{3}-\dfrac{1}{3}+1+0=2
\]
これは期待した結果になっている。