$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

微積分学の基本定理

$f(x)$を$1$変数関数であるとする。微積分学の基本定理（The fundamental theorem of Calculus）は以下のような式が成り立つという主張である。

$$\begin{equation} \int_a^b\left(\dfrac{\rmd f}{\rmd x}\right)\rmd x=f(b)-f(a)\tag{54} \end{equation}$$

もしこの形に馴染めなければ、$F(x)=\rmd f/\rmd x$とおいて、

$$\int_a^bF(x)\rmd x=f(b)-f(a)$$

と書くと良い。基本定理はどのように$F(x)$を積分するのかということを教えてくれる。つまり、微分した結果が$F(x)$に一致するような$f(x)$を探すということである。

幾何学的には、(33)のように、$\rmd f=(\rmd f/\rmd x)\rmd x$は$x$を$x+\rmd x$へ微小変化させたときの$f$の微小変位である。図1.25のように、基本定理(54)はもし$a$から$b$までの間隔を長さ$\rmd x$の微小な短冊に区切って増加分$\rmd f$を足し合わせると、結局、合計の変位は当然$f(b)-f(a)$になるということを言っているのである。換言すれば、変位を求める場合、微小変位を足し合わせるという方法と、一番最後の値から一番最初の値を引くという方法で$2$つの方法があるということである。どちらの方法でも、同じ答えが得られる。

基本定理の基本的な形式は、ある領域内の導関数の積分は、端点（境界）での関数の値で与えられる。ベクトル解析では、$3$種類の微分、すなわち、勾配、発散、回転があるので、それぞれに同じような形の基本定理が存在する。以下では、これらの定理の意味を説明して、尤もらしいと納得することにして、証明は行わない。

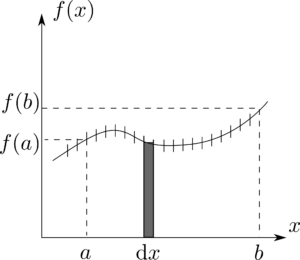
図1.25

勾配における基本定理

$3$変数のスカラー関数$T(x,y,z)$を考える。図1.26のように、$\bmsa$を始点として微小変位させる。このときの微小変位を$\rmd\bmsl_1$とする。(37)に依れば、関数$T$は以下の式に従って変化する。

$$\rmd T=(\nabla T)\cdot\rmd\bmsl_1$$

そしてまた更に微小変位させる。このときの微小変位を$\rmd\bmsl_2$とすると、このときの変位は$(\nabla T)\cdot\rmd\bmsl_2$となる。この方法を継続して微小変位をどんどん足し合わせていくことで終点$\bmsb$まで到達する。各点で$T$の勾配と変位$\rmd\bmsl$の内積を計算すると$T$の変化が得られる。結果的に、$\bmsa$から$\bmsb$を結ぶある経路での$T$の合計の変化分は

$$\begin{equation} \int_{\bmsa}^{\bmsb}(\nabla T)\cdot\rmd\bmsl=T(\bmsb)-T(\bmsa)\tag{55} \end{equation}$$

となる。これを勾配における基本定理（fundamental theorem for gradients）という。常微分での基本定理のように、導関数の積分（ここでは線積分）は境界$\bmsa$と$\bmsb$での関数の値で与えられることになる。

幾何学的には、例えば東京タワーの高さを決めたいとき、階段を登りながら$1$段$1$段の高さを測って足していくというのが(55)の左辺に対応しており、高度計を置いて頂点から地表までの差を測るというのが(55)の右辺に対応しているということである。基本定理の教えるところによって、どちらのやり方でも同じ答えが得られるようになっている。

加えて、前に問題で見たように、線積分は通常、$\bmsa$から$\bmsb$までの経路の取り方に依存する。しかし、(55)の右辺は経路の取り方に依存しておらず、始点と終点のみに依る結果となっている。明らかに、勾配には、勾配の線積分が経路に依存しないという特別な性質がある。これは以下のように書ける。

系1：$\displaystyle\int_{\bmsa}^{\bmsb}(\nabla T)\cdot\rmd\bmsl$は$\bmsa$から$\bmsb$までの経路の取り方と独立である。

系2：始点と終点が一致するため、$\displaystyle\oint(\nabla T)\cdot\rmd\bmsl=0$が成り立ち、このとき$T(\bmsb)=T(\bmsa)=0$である。

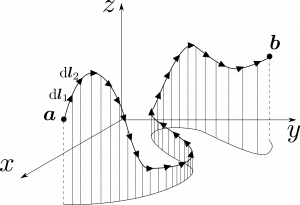
図1.26

問題

図1.27のように、原点$\bmsa=(0,0,0)$から$\bmsb=(2,1,0)$までの経路をとり、スカラー関数$T=xy^2$について、勾配における基本定理を確認せよ。

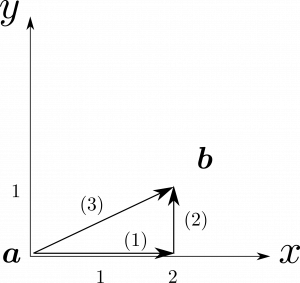
図1.27

解説

以下のように経路(1)と経路(2)を合わせた経路と、経路(3)で比較してみる。このとき常に、$\rmd\bmsl=\rmd x\hbx+\rmd y\hby+\rmd z\hbz$、$\nabla T=y^2\hbx+2xy\hby$である。

経路(1)
$y=0$、$\rmd\bmsl=\rmd x\hbx$、$\nabla T\cdot\rmd\bmsl=y^2\rmd x=0$なので、以下のようになる。

$$\int_{(1)}\nabla T\cdot\rmd\bmsl=0$$

経路(2)
$x=2$、$\rmd\bmsl=\rmd y\hby$、$\nabla T\cdot\rmd\bmsl=2xy\rmd y=4y\rmd y$なので、以下のようになる。

$$\int_{(2)}\nabla T\cdot\rmd\bmsl=\int_0^24y\rmd y=2y^2\biggr|_0^2=2$$

従って、線積分の値の合計は$2$である。これは$T(\bmsb)-T(\bmsa)=2-0=2$であるので、基本定理と一貫した結果となっている。

これだけで計算結果が経路に依らないことは確信出来るが、ここで更に$\bmsa$と$\bmsb$をまっすぐ結んだ経路(3)での積分計算を行ってみよう。

経路(3)
$y=\frac{1}{2}$、$\rmd y=\frac{1}{2}\rmd x$、$\nabla T\cdot\rmd\bmsl=y^2\rmd x+2xy\rmd y=\frac{3}{4}x^2\rmd x$なので、以下のようになる。

$$\int_{(3)}\nabla T\cdot\rmd\bmsl=\int_0^2\dfrac{3}{4}x^2\rmd x=\dfrac{1}{4}x^3\biggr|_0^2=2$$