$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

第４回、第５回に引き続き、ベクトル解析の復習、特にベクトル代数の3重積の解説を行います。
ここでは1回だけ行列式が出てきますが、$3$行$3$列の行列式の展開計算さえ覚えていれば理解出来ると思います。

3重積

ベクトルの外積は2つのベクトルから新たなベクトルを創る演算であるから、そのベクトルと新たなベクトルで内積や外積を計算する3重積（triple products）を構成することが出来る。

(1) スカラー3重積$\bma\cdot(\bmb\times\bmc)$

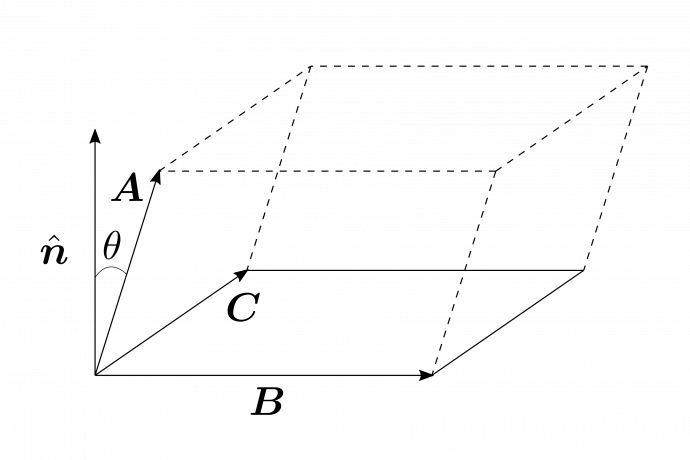
図1.12のように、幾何学的には、$|\bmb\times\bmc|$は底面の面積に、$|\bma\cos{\theta}|$は高さに等しいから、$|\bma\cdot(\bmb\times\bmc)|$はベクトル$\bma$、$\bmb$、$\bmc$で張られる平行六面体（parallelpiped）の体積に一致する。\\

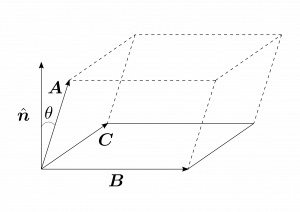図1.12

このことを考えると、
$$\bma\cdot(\bmb\times\bmc)=\bmb\cdot(\bmc\times\bma)=\bmc\cdot(\bma\times\bmb)\tag{15}$$
が明らかに成り立つ。左辺・中辺・右辺、どれも図1.12の図形の体積をあらわしているためである。但し、アルファベットの順番が循環していることに注意しなければならない。実際、アルファベット順になっていないスカラー3重積
$$\bma\cdot(\bmc\times\bmb)=\bmb\cdot(\bma\times\bmc)=\bmc\cdot(\bmb\times\bma)$$
では、符号が逆になってしまう。成分を綺麗に見るためには行列式を用いて、
$$\bma\cdot(\bmb\times\bmc)=\left| \begin{array}{ccc} A_x&A_y&A_z\\ B_x&B_y&B_z\\ C_x&C_y&C_z \end{array} \right|\tag{16}$$
と書けば良い。内積はどちらを先にしてどちらを後にしても良いから、$\bma\times\bmb$を1つのベクトルとみなせば直ちに以下が成り立つと分かる。
$$\bma\cdot(\bmb\times\bmc)=(\bma\times\bmb)\cdot\bmc$$
しかし、スカラー3重積の計算は括弧の位置が重要であるということに注意しなければならない。$(\bma\cdot\bmb)\times\bmc$はナンセンスである。スカラーとベクトルの外積を取ることは出来ないからだ。

(2) ベクトル3重積$\bma\times(\bmb\times\bmc)$

ベクトル3重積は以下のように、「$\bmb\bma\bmc-\bmc\bma\bmb$ルール」と呼ばれる形で簡単に書くことが出来る。
$$\bma\times(\bmb\times\bmc)=\bmb(\bma\cdot\bmc)-\bmc(\bma\cdot\bmb)\tag{17}$$
但し、ここでも括弧の位置が重要で、
$$(\bma\times\bmb)\times\bmc=-\bmc\times(\bma\times\bmb)=-\bma(\bmb\cdot\bmc)+\bmb(\bma\cdot\bmc)$$
となること、つまり、外積ではベクトルの順番をひっくり返すと符号が変わるということに注意せよ。4つ以上のベクトルを用いた全てのベクトルの積は(1.17)のように簡単に書き直すことが出来る。
従って、例えば以下のように、何回も外積の計算をする必要がないように簡単な内積の式に分解することが出来る。
$$\left\{ \begin{array}{lcl} (\bma\times\bmb)\cdot(\bmc\times\bmd)&=&(\bma\cdot\bmc)(\bmb\cdot\bmd)-(\bma\cdot\bmd)(\bmb\cdot\bmc)\\ &&\\ \bma\times[\bmb\times(\bmc\times\bmd)]&=&\bmb[\bma\cdot(\bmc\times\bmd)]-(\bma\cdot\bmb)(\bmc\cdot\bmd) \end{array} \right. \tag{18}$$