$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$

微分学

常微分

$1$つだけ変数をもつ関数$f(x)$を考えよう。この関数の常微分（ordinary derivative）$\rmd f/\rmd x$から何が得られるだろうか？答えは、変数$x$を微小量$\rmd x$だけ動かしたとき、関数$f(x)$がどれだけ急激に変化するかということ、である。これは次の式からも分かる。

\begin{equation}
\rmd f=\left(\dfrac{\rmd f}{\rmd x}\right)\rmd x\tag{33}
\end{equation}

もしも$x$を微小量$\rmd x$だけ増加させれば、$f$も微小量$\rmd f$だけ変化する。微分はこの比例係数をあらわしている。例えば、図1.17(a)では関数$f(x)$は$x$について緩やかに変化しているから、微分もこれに対応して小さい。一方で、図1.17(b)では関数$f(x)$は$x$について急激に変化しているから、$x=0$から離れるにつれて微分も大きくなっている。

幾何学的には、導関数$\rmd f/\rmd x$は$x$に対する$f$のグラフの傾きをあらわしている。

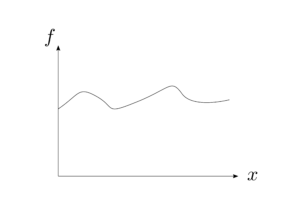
図1.17(a)

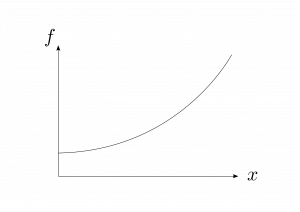
図1.17(b)

勾配

次に$3$つの変数を持つ関数を考えよう。ここでは室内の温度の関数$T(x,y,z)$を考えてみる。部屋のある角を原点にして座標軸を設ければ、室内の各点の温度が分かるだろう。先ほどの導関数$\rmd f/\rmd x$を一般化して変数が$3$つの関数$T(x,y,z)$でも使えるようにしたい。

微分は、位置が微小量変化したときに関数がどれくらい急激に変化するかをあらわしていると考えられる。しかし、今の場合は変数が$1$つの場合と違って、位置がどの方向に微小変化するのかという問題があるため、より複雑になっている。

もし位置が高くなれば温度は急激に上がり、位置が水平に変化すれば温度は大して変わらないと思われる。実際、温度$T$がどのように変化するのか？という問題は、どの方向に変化させるのかで答えが変わってくるのだ。

幸運なことに、実はこれは見た目ほど難しい問題ではない。偏微分の基本定理に依れば、

\begin{equation}
\rmd T=\left(\dfrac{\partial T}{\partial x}\right)\rmd x+\left(\dfrac{\partial T}{\partial y}\right)\rmd y+\left(\dfrac{\partial T}{\partial z}\right)\rmd z\tag{34}
\end{equation}

が成り立つ。このことは、$3$つの変数全てがそれぞれ$\rmd x$、$\rmd y$、$\rmd z$だけ微小変化したときに温度$T$がどのように変化するかをあらわしている。無限個の微分が必要ではないということは注目に値する。つまり、$3$次元座標の方向それぞれに沿った偏微分（partial derivative）がありさえすれば良いのだ。

(34)は以下の式のように、内積を連想させる。

\begin{equation}
\rmd T=\left(\dfrac{\partial T}{\partial x}\hbx+\dfrac{\partial T}{\partial y}\hby+\dfrac{\partial T}{\partial z}\hbz\right)\cdot(\rmd x\hbx+\rmd y\hby+\rmd z\hbz)=(\nabla T)\cdot(\rmd \bmsl)\tag{35}
\end{equation}

但し、

\begin{equation}
\nabla T\coloneqq\dfrac{\partial T}{\partial x}\hbx+\dfrac{\partial T}{\partial y}\hby+\dfrac{\partial T}{\partial z}\hbz\tag{36}
\end{equation}

であり、これは$T$の勾配（gradient）と呼ばれる。この$\nabla T$は$3$つの成分を持ったベクトル量であり、(35)は(33)を$3$次元の場合に一般化した微分であったのだということに注目せよ。

勾配は、幾何学的には、任意のベクトルのように大きさと向きを持つものである。その幾何学的意味を明らかにするために、まず内積の式(35)を(1)を用いて以下のように書き直す。

\begin{equation}
\rmd T=\nabla T\cdot\rmd\bmsl=|\nabla T||\rmd\bmsl|\cos{\theta}\tag{37}
\end{equation}

但し、$\theta$は$\nabla T$と$\rmd \bmsl$の間の角である。もし、長さ$|\rmd \bmsl|$を固定して$\theta$を変化させたとき、$\cos{\theta}=1$となる角度$\theta=0$で$\rmd T$は最大となる。つまり、距離$|\rmd\bmsl|$を固定したなら、$\rmd T$は$\nabla T$と同じ方向へ動かしたときに最大となる。従って、以下の$2$つが言える。

• 勾配$\nabla T$は関数$T$が最も増加する方向を向く。
• 大きさ$|\nabla T|$はこの最も増加する方向に沿った傾き（変化の割合）を与えてくれる。

丘の中腹に立っている自分を想像してみよう。

周りを見回して最も急な上り坂を見出せ。それは勾配の向きである。そして、その方向の傾斜、つまり平均変化率を測ってみよ。それはこの勾配の大きさである（先ほどと違って、ここでの関数は丘の高さであるから、緯度と経度のみに依存している。

つまりこの関数は$2$変数ではなく$3$変数であるが、勾配の幾何学的な意味はこちらの場合の方がより理解しやすい。）。(37)から分かるように、最も急な下り坂の方向は最も急な上り坂の方向の正反対の方向である。

これに対して、直角の方向、$\theta=90^\circ$では勾配は$0$となる。つまり、勾配は等高線に対して直交している。外面はこれらの性質を持たないと思いつくかもしれないが、外面にはねじれがあり、そこが微分不可能な関数に対応している。

勾配が$0$というのは、どのような意味があるのだろうか？

もし、$(x,y,z)$で$\nabla T=\bm{0}$であるならば、$(x,y,z)$から微小変位した点において$\rmd T=0$である。これはつまり、関数$T(x,y,z)$の停留点（stationary point）である。

これは最大値（頂点）、最小点（谷底）、鞍点（峠）、あるいは山の肩のいずれかである。これは$1$変数の関数の場合に導関数が$0$の点が最大点、最小点、あるいは変曲点を示していたことと類似している。

特に、$3$変数関数の極値を見つけたい場合にはその勾配を$0$に設定する必要がある。

問題

位置ベクトルの大きさ$r=\sqrt{x^2+y^2+z^2}$の勾配を求めよ。

解説

以下のように計算する。

\begin{align}
\nabla r=&\dfrac{\partial r}{\partial x}\hbx+\dfrac{\partial r}{\partial y}\hby+\dfrac{\partial r}{\partial z}\hbz\nonumber\\
=&\dfrac{1}{2}\dfrac{2x}{\sqrt{x^2+y^2+z^2}}\hbx+\dfrac{1}{2}\dfrac{2y}{\sqrt{x^2+y^2+z^2}}\hby+\dfrac{1}{2}\dfrac{2z}{\sqrt{x^2+y^2+z^2}}\hbz\nonumber\\
=&\dfrac{x\hbx+y\hby+z\hbz}{\sqrt{x^2+y^2+z^2}}=\dfrac{\bmsr}{r}=\hbr\nonumber
\end{align}

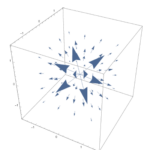
この結果は、原点からの距離は動径方向で最も急激に増加し、増加の比率は動径方向で$1$になることを示している。これは理にかなっている結果である。