$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\car}{\mathcal{R}}
\newcommand{\bcar}{\bm{\mathcal{R}}}
\newcommand{\hcar}{\bm{\hat{\mathcal{R}}}}
\newcommand{\hbx}{\bm{\hat{x}}}
\newcommand{\hby}{\bm{\hat{y}}}
\newcommand{\hbz}{\bm{\hat{z}}}
\newcommand{\hbr}{\bm{\hat{r}}}
\newcommand{\hbtheta}{\bm{\hat{\theta}}}
\newcommand{\hbphi}{\bm{\hat{\phi}}}
\newcommand{\hbs}{\bm{\hat{s}}}
\newcommand{\bmsa}{\bm{a}}
\newcommand{\bmsb}{\bm{b}}
\newcommand{\bmsc}{\bm{c}}
\newcommand{\bmsd}{\bm{d}}
\newcommand{\bmse}{\bm{e}}
\newcommand{\bmsf}{\bm{f}}
\newcommand{\bmsg}{\bm{g}}
\newcommand{\bmsh}{\bm{h}}
\newcommand{\bmsi}{\bm{i}}
\newcommand{\bmsj}{\bm{j}}
\newcommand{\bmsk}{\bm{k}}
\newcommand{\bmsl}{\bm{l}}
\newcommand{\bmsm}{\bm{m}}
\newcommand{\bmsn}{\bm{n}}
\newcommand{\bmso}{\bm{o}}
\newcommand{\bmsp}{\bm{p}}
\newcommand{\bmsq}{\bm{q}}
\newcommand{\bmsr}{\bm{r}}
\newcommand{\bmss}{\bm{s}}
\newcommand{\bmst}{\bm{t}}
\newcommand{\bmsu}{\bm{u}}
\newcommand{\bmsv}{\bm{v}}
\newcommand{\bmsw}{\bm{w}}
\newcommand{\bmsx}{\bm{x}}
\newcommand{\bmsy}{\bm{y}}
\newcommand{\bmsz}{\bm{z}}
\newcommand{\bma}{\bm{A}}
\newcommand{\bmb}{\bm{B}}
\newcommand{\bmc}{\bm{C}}
\newcommand{\bmd}{\bm{D}}
\newcommand{\bme}{\bm{E}}
\newcommand{\bmf}{\bm{F}}
\newcommand{\bmg}{\bm{G}}
\newcommand{\bmh}{\bm{H}}
\newcommand{\bmi}{\bm{I}}
\newcommand{\bmj}{\bm{J}}
\newcommand{\bmk}{\bm{K}}
\newcommand{\bml}{\bm{L}}
\newcommand{\bmm}{\bm{M}}
\newcommand{\bmn}{\bm{N}}
\newcommand{\bmo}{\bm{O}}
\newcommand{\bmp}{\bm{P}}
\newcommand{\bmq}{\bm{Q}}
\newcommand{\bmr}{\bm{R}}
\newcommand{\bms}{\bm{S}}
\newcommand{\bmt}{\bm{T}}
\newcommand{\bmu}{\bm{U}}
\newcommand{\bmv}{\bm{V}}
\newcommand{\bmw}{\bm{W}}
\newcommand{\bmx}{\bm{X}}
\newcommand{\bmy}{\bm{Y}}
\newcommand{\bmz}{\bm{Z}}
\newcommand{\rmd}{\mathrm{d}}$

発散

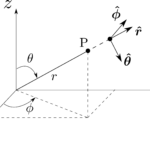
ナブラ演算子の定義から、発散を次のように定義する。

\begin{equation}
\nabla\cdot\bmsv=\left(\hbx\dfrac{\partial}{\partial x}+\hby\dfrac{\partial}{\partial y}+\hbz\dfrac{\partial}{\partial z}\right)\cdot(v_x\hbx+v_y\hby+v_z\hbz)=\dfrac{\partial v_x}{\partial x}+\dfrac{\partial v_y}{\partial y}+\dfrac{\partial v_z}{\partial z}\tag{40}
\end{equation}

ベクトル関数$\bmsv$の発散$\nabla\cdot\bmsv$はスカラーとなることに注意せよ。

なお、ベクトル関数$\bmsv(x,y,z)=v_x(x,y,z)\hbx+v_y(x,y,z)\hby+v_z(x,y,z)\hbz$は$3$つの実変数$x,y,z$についての関数であり、それぞれの点で各成分を有している。故にスカラー関数の発散のようなものは存在しないことも分かる。

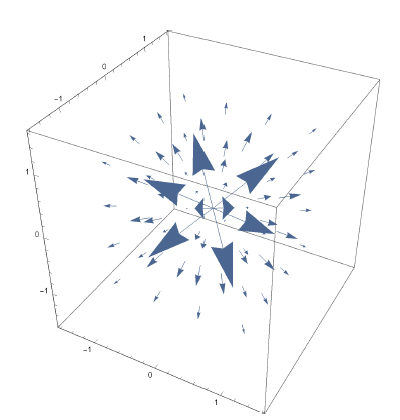
幾何学的にも発散というのはまさに適切な名前で、$\nabla\cdot\bmsv$はベクトル$\bmsv$がある点からどれくらい拡散するのかということを測る量である。

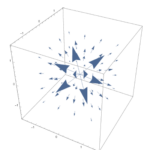
例えば、図1.18(a)は正の大きい発散を持っていて（もしもこれが点に吸い込まれる向きであれば発散は負となる。）、図1.18(b)は発散が$0$であり、図1.18(c)は正の発散量を持っている。

但し、いずれの図も代表的ないくつかの点における矢印のみを書いている。ベクトル$\bmsv$は位置の関数であり、いたるところで異なる値を持っているためである。

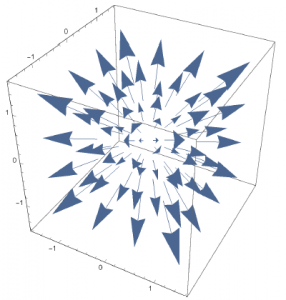
図1.18(a)

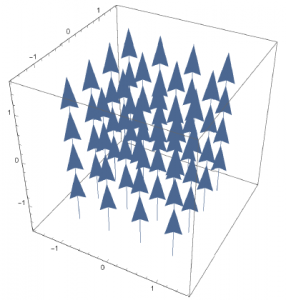
図1.18(b)

図1.18(c)

池の縁に立っていることを想像してみよう。水面の水の速さというベクトル$\bmsv$を知るにはどのようにすれば良いだろうか？

これを知るためには、木くずや葉っぱを池の水面に撒いてみて観察してみれば良い。それらが撒いた点から拡散していくなら正の発散を持っている。それらがある点に集まってくるなら負の発散を持っている。

この例え話は$2$次元の問題に過ぎないが、発散というものの意味が分かる教育的な例であるだろう。正の発散というのは蛇口のようなもので湧き出しを意味していて、負の発散というのは排水溝のようなもので吸い込みを意味している。

問題

図18の関数はそれぞれ、$\bmsv_a=\bmsr=x\hbx+y\hby+z\hbz$、$\bmsv_b=\hbz$、$\bmsv_c=z\hbz$である。これらの発散をそれぞれ計算せよ。

解説

以下のように計算する。

\[
\left\{
\begin{array}{lclclcl}
\nabla\cdot\bmsv_a&=&\dfrac{\partial}{\partial x}(x)+\dfrac{\partial}{\partial y}(y)+\dfrac{\partial}{\partial z}(z)&=&1+1+1&=&3\\
&&&&&&\\
\nabla\cdot\bmsv_b&=&\dfrac{\partial}{\partial x}(0)+\dfrac{\partial}{\partial y}(0)+\dfrac{\partial}{\partial z}(1)&=&0+0+0&=&0\\
&&&&&&\\
\nabla\cdot\bmsv_c&=&\dfrac{\partial}{\partial x}(0)+\dfrac{\partial}{\partial y}(0)+\dfrac{\partial}{\partial z}(z)&=&0+0+1&=&1
\end{array}
\right.
\]

これらは確かに先ほど説明した発散の値と一致しているから、それぞれ理にかなっている結果である。