$\def\bm#1{{\boldsymbol{#1}}}
\def\coloneqq{{:=}}
\newcommand{\rmd}{\mathrm{d}}$

振動する弦のモデル化

前回の復習

前回の変数分離法の計算で、

\begin{equation}
u(x,t)=\dfrac{1}{2}\biggl\{f^*(x-vt)+f^*(x+vt)\biggr\}\tag{35}
\end{equation}

という形に$u(x,t)$が書けることを見ました。イメージとしては下図のようになるのでしたね。

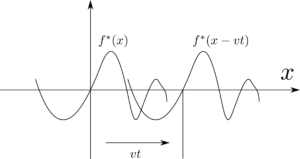
図4　式(35)の物理的解釈（再掲）

図のように、$f^*(x-vt)$のグラフは$f^*(x)$のグラフを右へ$vt$だけ移動させて得られます。従って、$f^*(x-vt)~(v>0)$は時間$t$の増加と共に右へ進行する波をあらわしています。同様に、$f^*(x+vt)$は左へ進行する波をあらわしています。つまり、$u(x,t)$はこれら$2$つの進行波の重ね合わせです。

これらの内容を基にして、今回はd’ Alembert の解法による解の求積を見ていきます。

波動論と音楽

d’ Alembert の解法による解の求積を見ていく前に、少し波動論と音楽の関係について見てみたいと思います。

これまでの議論から、波動方程式の解と高校物理における波動論の話の間に密接な関係があることは少なからず実感でしょう。波動論は音楽との関連も非常に深いものです。ここでは休憩も兼ねて、音楽への応用について簡単に述べることにしましょう。これまでの議論より、振動数は

\begin{equation}
f_n=\dfrac{\lambda_n}{2\pi}=\dfrac{vn}{2L}=\dfrac{n}{2L}\sqrt{\dfrac{T}{\rho}}\tag{36}
\end{equation}

で与えられます。振動数が高ければ高いほど、高い音を出す楽器となるので、張力$T$を変えれば調律ができることが分かるでしょう。故に、ギターやヴァイオリン、コントラバスなどの弦楽器は調律の際に張っている弦の張力を調整する仕組みになっているはずです。

しかし、張力は無限に大きくすることができないので別の工夫も必要となりますね。振動数を大きくするためには、張力$T$を大きくするほかに、線密度$\rho$を小さくする（弦を細くする）、あるいは弦を張る距離$L$を小さくするという$2$つの方法も考えられます。

ヴァイオリンとコントラバスを思い出してみましょう。ヴァイオリンは高い音を出せるように弦を張る距離（楽器の大きさ）は小さくなっていて、弦も細いものが用いられています。一方で、コントラバスは低い音を出せるように楽器の大きさは大きく、弦も太いものが用いられています。もしこれらの楽器を見る機会があれば、今回の内容を思い出しながら大きさに注目してみてください。

d’ Alembert の解法による解の求積

波動方程式(8)の解が式(35)で与えられました。この節では、式(8)を次の方法で変形すると式(35)が直接に得られることを示しましょう。新しい独立変数

\begin{equation}
y=x+vt、~~~z=x-vt\tag{37}
\end{equation}

を導入すると、$u$が$y$と$z$の関数になり、式(8)の偏導関数が$y$と$z$についての偏導関数であらわされることになります。連鎖法則から、

\begin{equation}
\dfrac{\partial u}{\partial x}=\dfrac{\partial u}{\partial y}\dfrac{\partial y}{\partial x}+\dfrac{\partial u}{\partial z}\dfrac{\partial z}{\partial x}
\end{equation}

となります。この式の右辺に再び連鎖法則を適用しましょう。ここで現れる全ての偏微分が連続とすると$\partial^2u/(\partial z\partial y)=\partial^2u/(\partial y\partial z)$です。$\partial y/\partial x=1$と$\partial z/\partial x=1$を用いると、

\begin{equation}
\dfrac{\partial^2u}{\partial x^2}=\dfrac{\partial}{\partial x}\left(\dfrac{\partial u}{\partial y}+\dfrac{\partial u}{\partial z}\right)=\dfrac{\partial}{\partial y}\left(\dfrac{\partial u}{\partial y}+\dfrac{\partial u}{\partial z}\right)\dfrac{\partial y}{\partial x}+\dfrac{\partial}{\partial z}\left(\dfrac{\partial u}{\partial y}+\dfrac{\partial u}{\partial z}\right)\dfrac{\partial z}{\partial x}=\dfrac{\partial^2u}{\partial y^2}+2\dfrac{\partial^2u}{\partial y\partial z}+\dfrac{\partial^2u}{\partial z^2}
\end{equation}

となります。同様のやり方で$t$についての$2$階偏導関数も計算すると

\begin{equation}
\dfrac{\partial^2u}{\partial t^2}=v^2\left(\dfrac{\partial^2u}{\partial y^2}-2\dfrac{\partial^2u}{\partial y\partial z}+\dfrac{\partial^2u}{\partial z^2}\right)
\end{equation}

となります。これら$2$つの結果を波動方程式(8)に代入すると、

\begin{equation}
\dfrac{\partial^2u}{\partial y\partial z}=0\tag{38}
\end{equation}

が得られる。d’ Alembert の解法の利点は、式(38)が積分を$2$回繰り返すことで簡単に解けるという点です。まず、$z$について積分すると、

\begin{equation}
\dfrac{\partial u}{\partial y}=h(y)
\end{equation}

となります。但し、$h(y)$は$y$の任意関数です。これを$y$について積分すると、

\begin{equation}
u(y、z)=\int h(y)dy+\psi(z)
\end{equation}

となります。但し、$\psi(z)$は$z$の任意関数である。積分は$y$のみの関数なので、この積分結果を$\phi(y)$とすると、$u$の解は$u=\phi(y)+\psi(z)$の形になります。式(37)を用いると、

\begin{equation}
u(x,t)=\phi(y)+\psi(z)=\phi(x+vt)+\psi(x-vt)\tag{39}
\end{equation}

となります。これが波動方程式(8)のd’ Alembert の解です。

初期条件を満たすd’ Alembert の解

ここでは以下の初期条件を課したd’ Alembert の解について議論します。

\begin{equation}
u(x,0)=f(x)\tag{40}
\end{equation}

\begin{equation}
\dfrac{\partial u}{\partial t}\biggr|_{t=0}=g(x)\tag{41}
\end{equation}

これは前に考えた初期条件と同じものです。式(39)を微分すると、

\begin{equation}
\dfrac{\partial u}{\partial t}=v\phi'(x+vt)-v\psi'(x-vt)\tag{42}
\end{equation}

が得られます。但し、プライム$’$は引数$x+vt$と$x-vt$についての微分です。式(39-42)から、

\begin{equation}
u(x,0)=\phi(x)+\psi(x)=f(x)\tag{43}
\end{equation}

\begin{equation}
\dfrac{\partial u}{\partial t}\biggr|_{t=0}=v\phi'(x)-v\phi'(x)=g(x)\tag{44}
\end{equation}

となります。式(44)を$v$で割って$x$で積分すると、

\begin{equation}
\phi(x)-\psi(x)=k(x_0)+\dfrac{1}{v}\int_{x_0}^xg(s)ds~~~\text{where}~k(x_0)=\phi(x_0)-\psi(x_0)\tag{45}
\end{equation}

となります。上式と式(43)を加えると$\psi$が消去されます。これを$2$で割って以下の式を得ることができます。

\begin{equation}
\phi(x)=\dfrac{1}{2}f(x)+\dfrac{1}{2v}\int_{x_0}^xg(s)ds+\dfrac{1}{2}k(x_0)\tag{46}
\end{equation}

同様に式(43)から式(45)を引いて$2$で割ると

\begin{equation}
\psi(x)=\dfrac{1}{2}f(x)-\dfrac{1}{2v}\int_{x_0}^xg(s)ds-\dfrac{1}{2}k(x_0)\tag{47}
\end{equation}

となります。式(46)で$x$を$x+vt$でおきかえると、積分は$x_0$から$x+vt$までになります。同様に式(47)で$x$を$x-vt$でおきかえると、積分は$x_0$から$x-vt$までになりますが、積分の符号を変えると積分範囲は$x-vt$から$x_0$までになります。このようにしておいて$\phi(x+vt)$と$\psi(x-vt)$を加えると、式(39)から$u(x,t)$が以下で与えられることが分かります。

\begin{equation}
u(x,t)=\dfrac{1}{2}\biggl\{f(x+vt)+f(x-ct)\biggr\}+\dfrac{1}{2v}\int_{x-vt}^{x+vt}g(s)ds\tag{48}
\end{equation}

特に初速度が$0$ならば、上式は、

\begin{equation}
u(x,t)=\dfrac{1}{2}\biggl\{f(x+vt)+f(x-ct)\biggr\}\tag{49}
\end{equation}

となります。これは式(35)と同じ結論です。境界条件(9)から、関数$f$は奇関数で周期$2L$を持つことも明らかでしょう。このように、$2$つの初期条件と境界条件から解が一意的に決定できます。

このd’ Alembert の解の導出は変数分離の方法よりも洗練されているだろう。しかし、d’ Alembert の解法は限定的で、Fourier 級数による解法は様々な偏微分方程式に利用することができます。