$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

$\hbr/r^2$の発散

以下のようなベクトル関数の発散を考えよう。

$$\begin{equation} \bmsv=\dfrac{1}{r^2}\hbr\tag{83} \end{equation}$$

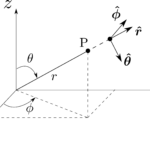
図1.44のように、いかなる場所でも$\bmsv$は動径外向き方向を向いている。もしこのベクトル関数が正の大きな発散を持っているのであればその通りであるのだが、実は(71)を用いて計算できるように、この発散を計算すると$0$になってしまう。

$$\begin{equation} \nabla\cdot\bmsv=\dfrac{1}{r^2}\dfrac{\partial}{\partial r}\left(r^2\dfrac{1}{r^2}\right)=\dfrac{1}{r^2}\dfrac{\partial}{\partial r}(1)=0\tag{84} \end{equation}$$

このベクトル関数に発散定理を適用すると、プロットは密になる。中心が原点に一致している半径$R$の球で積分すると仮定すると、このときの面積分は、

$$\begin{equation} \oint\bmsv\cdot\rmd\bmsa=\int\left(\dfrac{1}{R^2}\hbr\right)\cdot(R^2\sin{\theta}\rmd\theta\rmd\phi\hbr)=\left(\int_0^\pi\sin{\theta}\rmd\theta\right)\left(\int_0^{2\pi}\rmd\phi\right)=4\pi\tag{85} \end{equation}$$

となる。しかし、体積積分$\int\nabla\cdot\rmd\tau$は(84)を信じると$0$と分かる。これは発散定理が誤っていることを意味するのだろうか？ここで何が起こっているのだろうか？

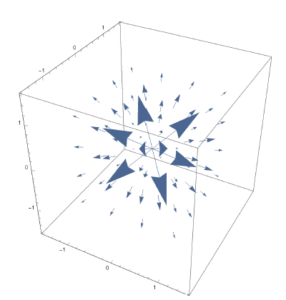
図1.44

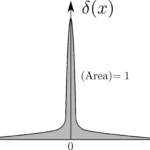
事の発端は$r=0$の点にある。この点では$\bmsv$は発散しているが、(84)では、これにより意図せず$0$で割り算を行っていることになっている。$\nabla\cdot\bmsv=0$が原点を除いて正しいということは確かだが、原点における場合はより複雑な問題となる。面積分は(85)は半径$R$の値とは関係がないということ、つまり、発散定理が正しければ中心が原点に位置しているようないかなる球でも$\int\nabla\cdot\bmsv\rmd\tau=4\pi$という値を得ることになることに注意せよ。球がどんなに小さくても良いのであるから、明らかに、全体の寄与は$r=0$の点に由来しているものであることになる。故に、$\nabla\cdot\bmsv$は原点という$1$点を除いて$0$となるのにその積分は（積分領域に原点を含んでいれば）$4\pi$という値になるという、奇怪な性質を持つことになる。通常の関数でこのような振る舞いを見せる関数は存在しない。他方で、物理的な例としては、質点の密度（単位体積当たりの質量）などが挙げられる。ここでつまずいてしまっている問題を解決するための関数は、物理学者の間ではDirac のデルタ関数（Dirac delta function）という数学的対象として知られている。これは理論物理学の様々なところで用いられている。更に、今考えているベクトル関数$\hbr/r^2$の発散という問題は不可解な好奇心による問題ではなく、実は、電磁気学の理論において中心となると言っても過言ではないくらい重要な問題である。従って、ここではこのDirac のデルタ関数とそれに関連する事柄について見ておくことにする。