$\def\bm#1{{\boldsymbol{#1}}} \def\coloneqq{{:=}} \newcommand{\car}{\mathcal{R}} \newcommand{\bcar}{\bm{\mathcal{R}}} \newcommand{\hcar}{\bm{\hat{\mathcal{R}}}} \newcommand{\hbx}{\bm{\hat{x}}} \newcommand{\hby}{\bm{\hat{y}}} \newcommand{\hbz}{\bm{\hat{z}}} \newcommand{\hbr}{\bm{\hat{r}}} \newcommand{\hbtheta}{\bm{\hat{\theta}}} \newcommand{\hbphi}{\bm{\hat{\phi}}} \newcommand{\hbs}{\bm{\hat{s}}} \newcommand{\bmsa}{\bm{a}} \newcommand{\bmsb}{\bm{b}} \newcommand{\bmsc}{\bm{c}} \newcommand{\bmsd}{\bm{d}} \newcommand{\bmse}{\bm{e}} \newcommand{\bmsf}{\bm{f}} \newcommand{\bmsg}{\bm{g}} \newcommand{\bmsh}{\bm{h}} \newcommand{\bmsi}{\bm{i}} \newcommand{\bmsj}{\bm{j}} \newcommand{\bmsk}{\bm{k}} \newcommand{\bmsl}{\bm{l}} \newcommand{\bmsm}{\bm{m}} \newcommand{\bmsn}{\bm{n}} \newcommand{\bmso}{\bm{o}} \newcommand{\bmsp}{\bm{p}} \newcommand{\bmsq}{\bm{q}} \newcommand{\bmsr}{\bm{r}} \newcommand{\bmss}{\bm{s}} \newcommand{\bmst}{\bm{t}} \newcommand{\bmsu}{\bm{u}} \newcommand{\bmsv}{\bm{v}} \newcommand{\bmsw}{\bm{w}} \newcommand{\bmsx}{\bm{x}} \newcommand{\bmsy}{\bm{y}} \newcommand{\bmsz}{\bm{z}} \newcommand{\bma}{\bm{A}} \newcommand{\bmb}{\bm{B}} \newcommand{\bmc}{\bm{C}} \newcommand{\bmd}{\bm{D}} \newcommand{\bme}{\bm{E}} \newcommand{\bmf}{\bm{F}} \newcommand{\bmg}{\bm{G}} \newcommand{\bmh}{\bm{H}} \newcommand{\bmi}{\bm{I}} \newcommand{\bmj}{\bm{J}} \newcommand{\bmk}{\bm{K}} \newcommand{\bml}{\bm{L}} \newcommand{\bmm}{\bm{M}} \newcommand{\bmn}{\bm{N}} \newcommand{\bmo}{\bm{O}} \newcommand{\bmp}{\bm{P}} \newcommand{\bmq}{\bm{Q}} \newcommand{\bmr}{\bm{R}} \newcommand{\bms}{\bm{S}} \newcommand{\bmt}{\bm{T}} \newcommand{\bmu}{\bm{U}} \newcommand{\bmv}{\bm{V}} \newcommand{\bmw}{\bm{W}} \newcommand{\bmx}{\bm{X}} \newcommand{\bmy}{\bm{Y}} \newcommand{\bmz}{\bm{Z}} \newcommand{\rmd}{\mathrm{d}}$

$1$次元におけるDirac のデルタ関数

$1$次元におけるDirac のデルタ関数$\delta(x)$は図1.45のように無限に長い針のような形で、面積が$1$であるとされる。つまり、以下の$2$式が成り立つことになる（デルタ関数$\delta(x)$の次元は積分変数の次元の逆数であるということに注意せよ。もし$x$が長さの次元を持っているのであれば、$\delta(x)$の次元は$\text{m}^{-1}$となる。）。

$$\begin{equation} \delta(x)=\left\{ \begin{array}{cr} 0&~~~~~\mathrm{if}~x\neq0\\ {\infty}&~~~~~\mathrm{if}~x=0 \end{array} \right\} \tag{86} \end{equation}$$

$$\begin{equation} \int_{-\infty}^\infty\delta(x)\rmd x=1\tag{87} \end{equation}$$

図1.45

厳密には、$\delta(x)$は$x=0$の点で有限の値とならないから関数ではない。このようなものは数学では一般化された関数（generalized function）とか、超関数（distribution）として知られている。図1.46のように、デルタ関数は高さが$n$で底辺が$1/n$の長方形$R_n(x)$を連続的に変形した極限であるとか、高さが$n$で底辺が$2/n$の二等辺三角形$T_n(x)$を連続的に変形した極限であると考えることも出来る。もしこちらの方が理解しやすければ、それでも良い。

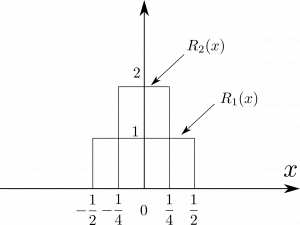
図1.46(a)

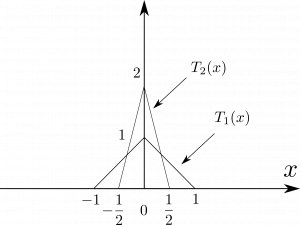
図1.46(b)

もし$f(x)$がある通常の関数であれば（これはもう$1$つのデルタ関数であったりしてはいけない。実は以下の式が成り立つためには、$f(x)$は連続関数である必要がある。）、$f(x)\delta(x)$の積は$x=0$を除くいたるところで$0$になるから、

$$\begin{equation} f(x)\delta(x)=f(0)\delta(x)\tag{88} \end{equation}$$

が成り立つ。これはデルタ関数における最も重要な事実であり、これによりデルタ関数と掛け算した関数についてはデルタ関数が無限大になる点の値のみを考えれば良いということが保証される。特に、以下が成り立つことになる。

$$\begin{equation} \int_{-\infty}^\infty f(x)\delta(x)\rmd x=f(0)\int_{-\infty}^\infty\delta(x)\rmd x=f(0)\tag{89} \end{equation}$$

積分の下では、デルタ関数は関数$f(x)$の$x=0$における値を抜き出すことになる（故に、これ以降は積分範囲も$-\infty$から$+\infty$ではなく、$-\epsilon$から$+\epsilon$とすれば十分である。）。

勿論、デルタ関数の針は図1.47のように原点$x=0$から$x=a$のところにずらしても良い。

図1.47

このとき、デルタ関数の式は

$$\begin{equation} \delta(x-a)=\left\{ \begin{array}{cr} 0&~~~~~\mathrm{if}~x\neq a\\ {\infty}&~~~~~\mathrm{if}~x=a \end{array} \right\}~~~\mathrm{with}~\int_{-\infty}^\infty\delta(x-a)\rmd x=1 \tag{90} \end{equation}$$

となり、(88)は以下のように書き換えられる。

$$\begin{equation} f(x)\delta(x-a)=f(a)\delta(x-a)\tag{91} \end{equation}$$

そして、(89)も以下のように一般化することが出来る。

$$\begin{equation} \int_{-\infty}^\infty f(x)\delta(x-a)\rmd x=f(a)\tag{92} \end{equation}$$

問題

次の積分を計算せよ。

$$\int_0^3x^3\delta(x-2)\rmd x$$

解説

デルタ関数は$x=2$における$x^3$の値を抜き出すから、積分の答えは$8$になる。もしも積分領域が$0$から$1$などで$2$が含まれていない場合は、デルタ関数の針が積分領域の外側に出ていることになるから、積分の値は$0$となる。

デルタ関数$\delta(x)$自身は正当な関数ではないが、$\delta(x)$の積分は関数として完全に受け入れることが出来る。実際、デルタ関数はいつも積分記号の中で利用されるものであると考えておくのが$1$番良い。特に、デルタ関数を含んだ$2$つの表現$D_1(x)$と$D_2(x)$において

$$\begin{equation} \int_{-\infty}^\infty f(x)D_1(x)\rmd x=\int_{-\infty}^\infty f(x)D_2(x)\rmd x\tag{93} \end{equation}$$

が全ての普通の関数$f(x)$成り立つ（積分は全ての$f(x)$において等しくなる必要があるということを強調しておく。$D_1(x)$と$D_2(x)$が$x=17$の近傍で違う振る舞いをする関数であると仮定してみる。このとき、$x=17$の付近で急激に大きくなる$f(x)$を扱うと、積分の値は異なってしまう。）のであれば、これらの表現は同等であると言う。

問題

以下の式が成り立つことを示せ。

$$\begin{equation} \delta(kx)=\dfrac{1}{|k|}\delta(x)\tag{94} \end{equation}$$

但し、$k$は非ゼロの任意の定数である（特に、$\delta(-x)=\delta(x)$となる。）。

解説

任意の試行関数$f(x)$において、以下の積分を考えてみる。

$$\int_{-\infty}^\infty f(x)\delta(kx)\rmd x$$

変数変換を$y=kx$として行う。このとき、$x=y/k$なので$\rmd x=(1/k)\rmd y$である。もし$k$が正の値をとるならば、積分変数$y$による積分は積分変数$x$による積分と同様に$-\infty$から$+\infty$にかけて行われる。もし$k$が負の値をとるならば積分変数$y$による積分は$+\infty$から$-\infty$にかけて行われる。この時の積分は当然$k$が正のときの結果と符号が揃うようになっている。故に、

$$\int_{-\infty}^\infty f(x)\delta(kx)\rmd x=\pm\int_{-\infty}^\infty f(y/k)\delta(y)\dfrac{\rmd y}{k}=\pm\dfrac{1}{k}f(0)=\dfrac{1}{|k|}f(0)$$

となる（負符号は$k$が負の値となる場合に適用される。そしてこのことを考慮して最右辺では$k$に絶対値を付けることで$\pm$を取り除き綺麗な形に直した。）。そして、積分記号の中では$\delta(kx)$は$(1/|k|)\delta(x)$と同じ役割を担うことになる。

$$\int_{-\infty}^\infty f(x)\delta(kx)\rmd x=\int_{-\infty}^\infty f(x)\left[\dfrac{1}{|k|}\delta(x)\right]\rmd x$$

故に、(93)より、$\delta(kx)$は$(1/|k|)\delta(x)$と同等になる。